生成扩散模型学习笔记一

首次学习根据苏剑林的生成扩散模型漫谈而来

GAN生成模型的拆楼建楼类比

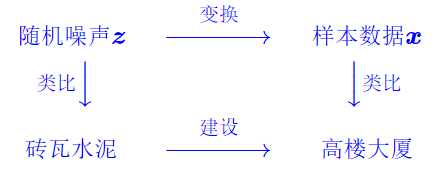
GAN根据随机噪声z变换一个样本数据x，将这个过程想象为建设高楼，那么随机噪声就是用于建楼的材料，样本数据就是我们需要盖的高楼大厦。变换的过程就是建楼的过程，而我们的生成模型就是用来变换随机噪声成样本数据的，也类似把砖瓦水泥做成高楼大厦的施工队。

显然建设高楼的过程不是那么容易，为了达到要求我们需要建楼的计划蓝图，这个怎么来呢？我们经常看见这样的故事，一个有天赋的孩子从小就喜欢拆东西然后试着自己拼接起来，最终成为一个伟大的发明家科学家等等，我们也要做类似的事情——拆。

根据结构将高楼大厦一步一步一步一步拆成零碎的砖瓦水泥，记住是一步步的，一口气拆掉跟直接爆破没啥区别，研究不出如何盖成这个大厦的。我们做出以下假设：

• x₀：建好的高楼大厦（数据样本）
• x_t：每一步拆除的结果（逆向变换过程）
• x_T：最终的砖瓦水泥（随机噪声）

拆楼的过程就是

x=x₀→x₁→x₂→⋯→x_T−1→x_T=z

其中我们将x_t-1→x_t的过程记为μ，也就是x_t-1=μ(x_t)，为什么呢？因为我们要根据每一步拆楼去反推每一步建楼的方法，这样我们就能够一步一步把大楼建起来~

总结以下，我们将生成模型视为建设大楼的施工队，先根据已有大楼一步一步拆解，反向研究如何一步一步搭建，给施工队指导从而一步一步建立大楼。

拆楼步骤

DDPM生成模型与上述类比一致，根据数据样本渐变到随机噪声，记录每一步变换最后得到逆变换从而一步一步完成数据样本生成（所以说DDPM应该理解为渐变模型更形象）。

DDPM的拆楼步骤建模如下：

x_t=α_tx_t−1+β_tε_t，ε_t∼N(0,I)

• α_t,β_t>0
• α_t²+β_t² = 1
• β_t究极接近于0
• β_t代表对原来楼体的破坏程度
• ε_t代表对原始信号的破坏，称之为噪声，也可以说是原材料

每一步“拆楼”中我们都将x_t−1拆解为“α_tx_t−1的楼体加上βtεt的原料”

反复执行拆楼步骤，可以得到以下式子（偷个懒直接放苏剑林大佬的原图）：

前面有一个条件是α_t²+β_t² = 1，接下来我们推导一下，我们的目的是根据这个条件得到上式x_i的系数平方之和恒为1，我们设x_i的系数平方为A_i（i=0，1，2 ... t），于是有以下：

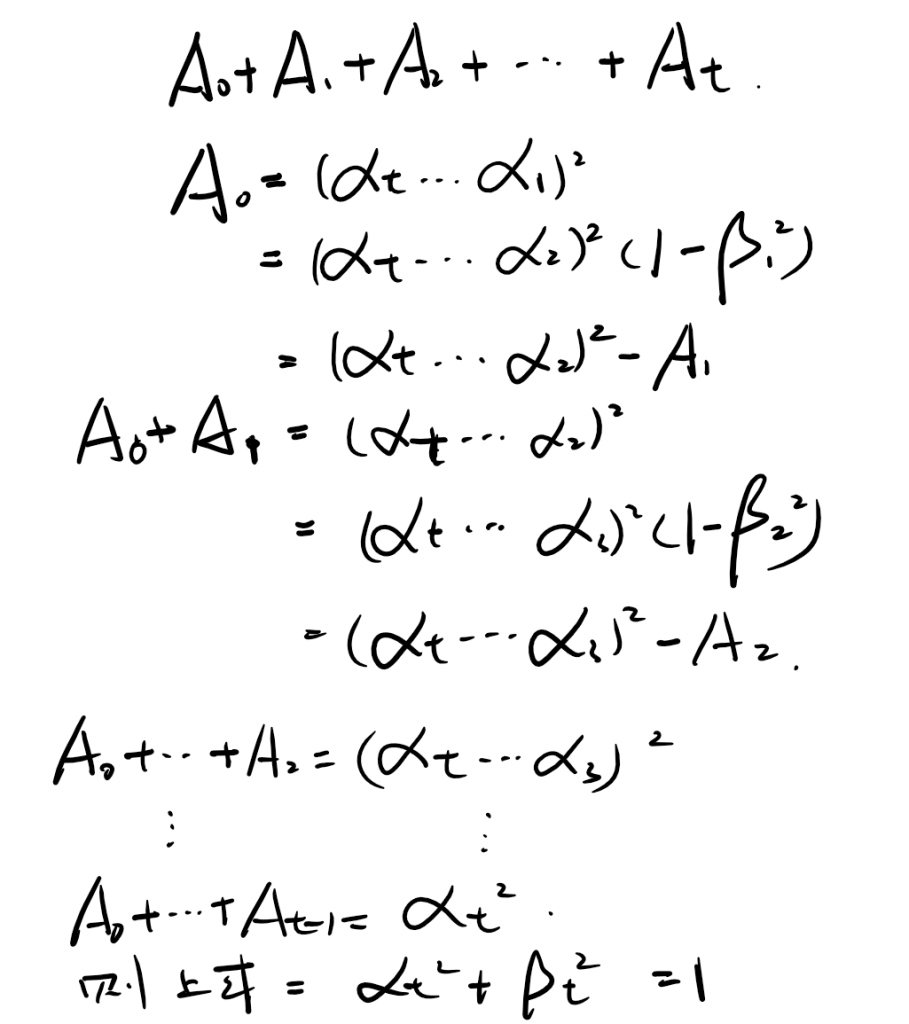
利用概率论的正态分布的叠加性，上述多个独立的正态噪声之和分布事实上是均值为0，方差为系数平方和（这里的系数不包括x₀的系数）的正态分布。于是我们有

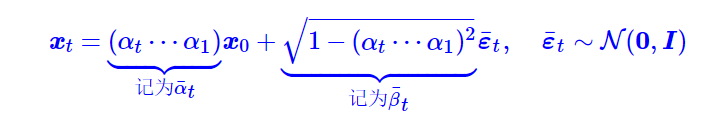
这样计算x_t就更加方便了。此外DDPM会选择合适的α_t使得，也就是说经过T步拆楼后剩下的楼体几乎可以忽略不计，几乎全部转化为原材料ε

建楼步骤

拆楼是从x_t-1到x_t，在这个过程中我们得到每一步变换的模型，那么反过来我们有了x_t→x_t−1的模型，记作μ(x_t)，容易想到的学习方案应当是最小化两者的欧式距离：

||x_t−1−μ(x_t)||²

接下来精细化这个一步骤，将我们的拆楼步骤建模倒过来写，可以写成：

于是我们将建楼模型μ(x_t)（直接将x_t-1代入即可）写作：

θ是训练参数，将这个式子代入欧氏距离的公式，得到：

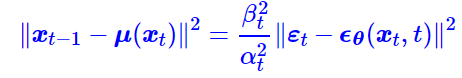
前部分的因子表示的是loss权重，暂时忽略掉。

所以我们现在有的东西如下：

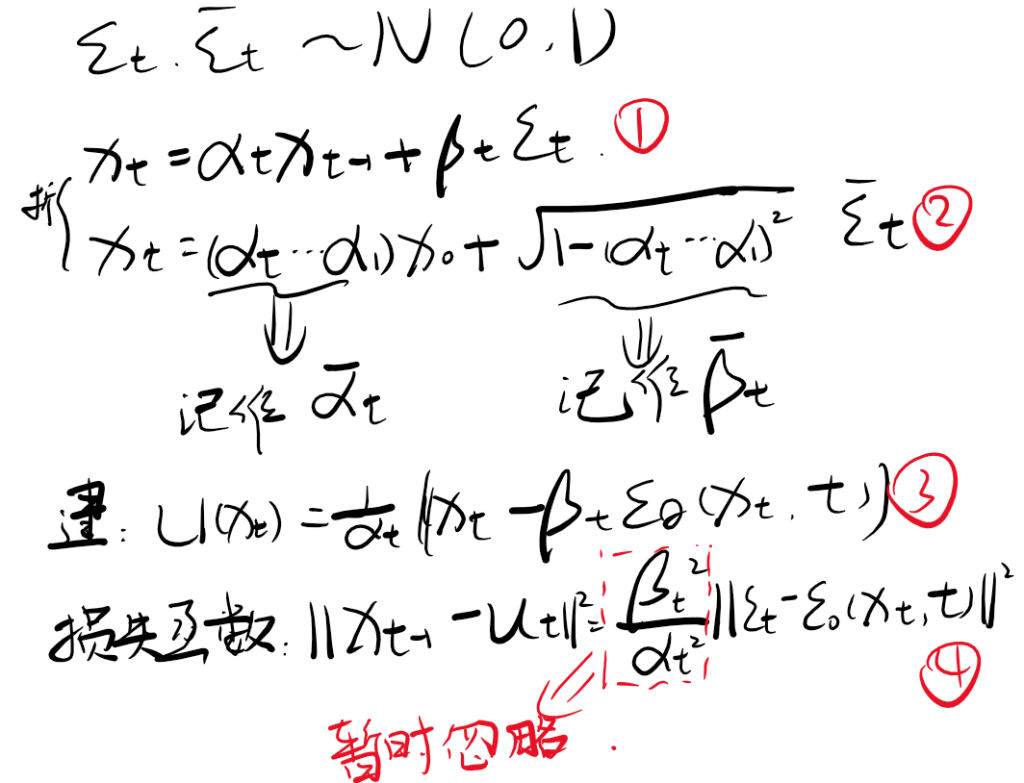
然后做以下推导：

也就是在这一步我们获得了损失函数的形式：

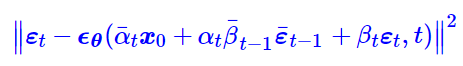
苏剑林提到这里退一步求x_t而非直接根据式2求是因为事先采样的是ε_t，而非式2中所需要的函数，总的来说以不可以独立采样2式所需，也就无法使用了。

降低方差

原理上得到以上的损失函数形式就可以完成DDPM训练了，不过在实际应用它存在方差过大的风险，收敛会慢很多，为什么呢？还是因为上式需要4个采样的随机变量！

需要采样的随机变量越多，损失函数的估计越模糊。于是我们需要尝试降低方差。给出的方法就是使正态分布的两个变量合并成一个正态随机变量。

由于正态分布的叠加性，我们可知

随缘更新中，等我学完学会... ...