Variational AutoEncoder (VAE)
VEA假设隐变量服从某种常见的分布概率(例如正态分布),进而训练出一个模型X=g(Z),这个,排序将原来的概率分布映射到训练集的概率分布,即分布的变换。
也就是先根据已经有的某种分布随机生成一组隐变量,这个隐变量经过生成器生成一组目标数据,使得这组数据和原目标分布数据非常接近。
难点在于如何确定生成的数据和目标数据接近的程度多少才是最好的。
生成模型
取得一组样品,根据这组样品X获得它的分布p(X),用这个分布p(X)随意采样生成目标结果。难点在于这个分布复杂难以确定,于是取隐变量Z,Z可以生成X。假设Z满足一个分布概率(如正态分布),则可以从正态分布中随机取Z,用Z和X的关系算出p(X)。
p(X)=Σzp(X|Z)p(Z)
也就是说不直接求p(X),而是构造其他变量(也就是隐变量),获得它与X的关系,再计算出p(X)。其中p(X|Z)为后验分布,p(Z)为先验分布。
VAE的核心
不仅仅假设p(Z)是正态分布,且假设每个p(Xk|Z)也是正态分布。也就是对X采样有X={X1,X2,X3......Xk},针对每个Xk都获取一个专属于它和Z的正态分布。也就是有k个X样品就有k个正态分布p(Xk|Z)。
如何获取这k个正态分布?那就是拟合。
如何确定这个正态分布呢?那就是均值和方差,用数据与假设的Z学均值和方差。
学到这k个正态分布后,从p(Z|Xk)中采样一个Zk,学习获取Xk=g(Zk)。接下来只需要优化最小方差即可。
VAE中的Variational
由于通过优化最小方差来训练生成器,最终使得模型的生成数据和真实数据趋近,但是由于Zk是随机采样过的而非通过均值和方差学习所得,所以Z是有噪声的,噪声实际就是用方差度量。为使得学习尽量接近必须使噪声变小。
那么能够让噪声的方差为0吗?
不可以!!!
因为需要给模型训练难度,否则模型只会学习高斯分布的均值从而失去随机性,VAE就变成了AE。所以需要再AE前加上一个Variational使得方差持续存在也就是噪声持续存在。如何解决这个问题,只需要使得方差永远存在就行,VAE就是使得p(Z|X)趋于正态分布N(0,I)。为什么呢?因为一个公式:
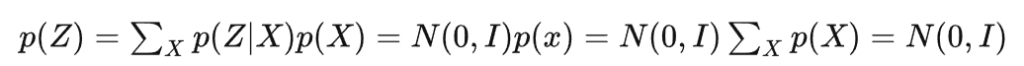
只需要保证p(Z|X)都趋于N(0,I),那么就可以保证p(Z)也趋于N(0,I),从而实现先验假设,构成一个闭环。如何做到这点呢?那就是加loss(抱歉我现在不理解)。
VAE的本质
VAE其实就是再AE的基础上对均值学习添加了高斯噪声(正态分布的随机采样),使得生成器具有噪声鲁棒性。为防止噪声小时,将所有p(Z|X)区域标准正态分布并且使得均值降为0但是方差仍然包吃住。这个时候如果训练效果不好就降低噪声,逐渐拟合时增加噪声。
扩散模型,DM(Diffusion Model)
事实上DM就是对VAE的升级版本。
VAE必须要设计一个g(Z)=X,那么最终后验p(X|Z)的表达能力和计算代价不可兼得,也就是说简单后验表达不丰富,但是复杂后验又太复杂。
而GAN就是简单粗暴不需要Z直接训练生成器,唯一难度就是生成的数据和真实数据是否相等以及相等设定程度不好设置。
DM其实就是借鉴GAN的训练单一思路和VAE不需要判别器的隐变量变分思路糅合。
正态分布
表型特征为中间高两边低的概率分布,图像为钟型曲线。其函数表达式如下:
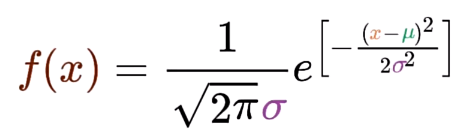
从一个均值为0标准差为1的标准正态分布中随机抽取样本,生成一组符合该分布的随机变量值,这组变量称为标准正态分布随机变量,这样的随机变量也被称作“高斯噪声”。扩散模型也就是向图片中逐步加入高斯噪声,前向加噪后再逆向去噪生成图片。
在生成模型中这个过程通过图像的三原色数据与标准颜色差进行。
此外,噪声与原图数据占比此消彼长,因此通过噪声细节能够很好地模拟扩散过程(物质从高浓度向低浓度逐步扩散的过程),不断给原图注入噪声,一直到原图不在清晰。在这个迭代过程中噪声的大小是不断增大的。
问题:是否能够不迭代直接获得最后的图像呢?






Comments NOTHING