第一天简单了解一下数学建模是什么东西,以及学习组成和学习方法~简单来说,之后以算法,编程,写作,排版来学习~
数学模型是什么
原型和模型
原型
- 人们在现实世界操纵管理的对象(比如工业品,汽车,
社畜等等) - 文学作品里某个人物形象的来源(如阿Q原型是那个时代软糯的中国人)
- 能够得出某些规律的事物
模型
模型是指为了某个特定目的将原型的某一部分信息简缩,提炼构造的原型替代物,是对所研究的系统,过程,事物或概念的一种表达形式,也可指根据实验,图样放大或缩小而制作的样品,一般用于展览或实验或铸造机器零件等用的模子。说白了就是生产原型得出解决某一类问题的万用模板。
分类
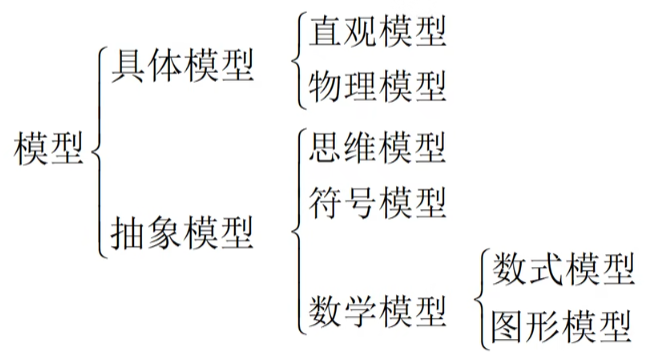
数学建模重点研究的是数式模型和图形模型
定义
官方解释:利用数学方法解决实际问题的一种实践(这不是废话吗)
通俗解释:用数学分析问题(不是 数学分析/问题 哈,是 数学/分析问题,让我想起数学分析这个令人不愉快科目了)
认识误区
- 高大上,入手极其难
- 时间长,一年才能入手
- 人难找,队友飘忽不定
- 没啥用,拿奖完事大吉(至少对写论文有用)
- 资料整理极其不用
- 背景多,高数线代全上(有算法有编程而且是部分算法需要底子深)
大概步骤
第一步》》模型假设
针对问题特点和建模目的,做出合理的简化的假设(在合理与简化间做出折中)
第二步》》建立模型
用数学的语言符号描述问题,发挥想象力(尽量采用简单的数学工具)
过程
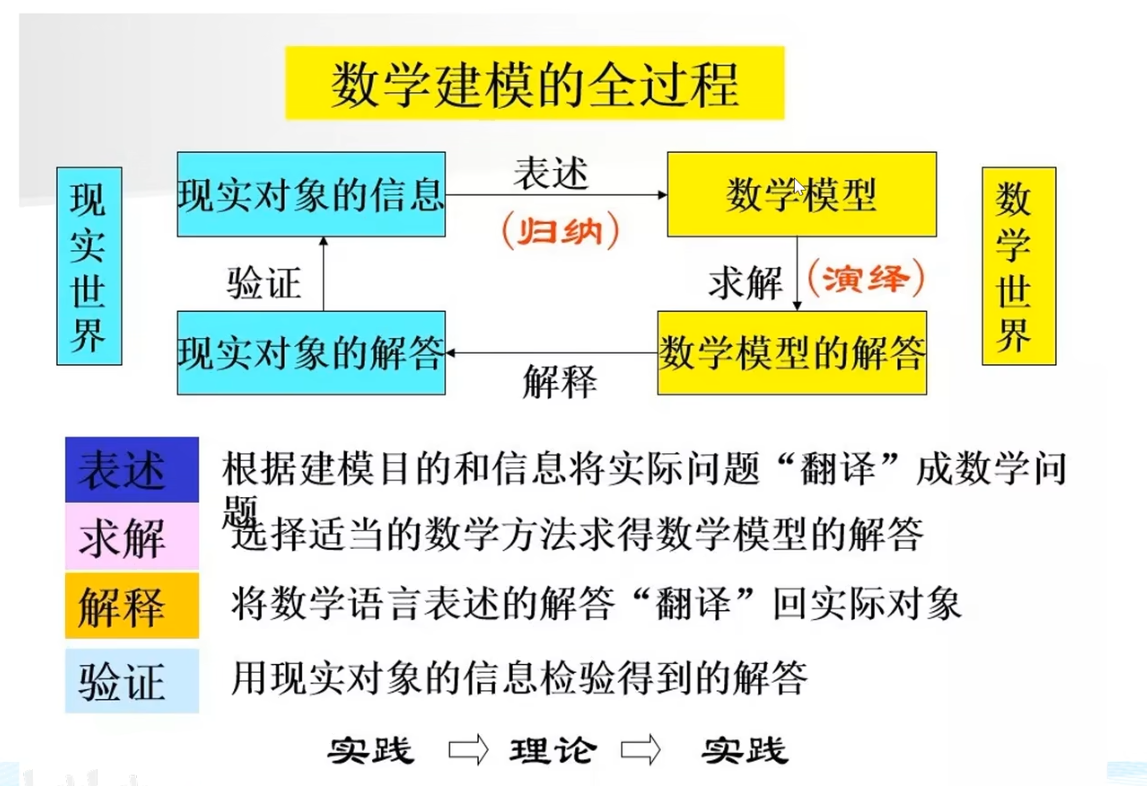
题目——摘要,关键词——问题重述(用自己的理解语言)——问题假设——问题分析——符号说明——模型建立——模型优缺点评价——参考文献
如何学习?
掌握固定模式,多看高水平或优秀论文,一定不要直接抄袭问题,问题假设在只要对我们的结果有影响,但是小概率并且难以寻找
按照 算法——编程——写作——排版 顺序学习
- 算法:课程+数学建模的书
- 编程:matlab
- 写作:整理优秀论文对语言进行学习
- 排版:LATEX或word
数学建模六个步骤
模型准备
解决问题的实际背景,明确其实际意义,掌握对象的各种信息。以数学思路来解决问题的精髓。数学思路贯穿问题的全过程,进而用数学语言来描述问题。要求符合数学理论,符合数学习惯,清晰准备。解决实际问题之后搜集资料,快速阅读和理解参考文献。翻译一下:理解和分析问题,将问题转化为数学语言,并且提前备好相关知识和资料。
模型假设
根据实际对象的特征和建模目的,将问题进行有必要的简化,并用精确的语言提出一些恰当的假设,对设计到的变量,变量的单位,相关假设进行定义,用表达式将其表达出来。翻译一下:将问题精简假设适用的模型,变量,定义和表达式。
模型建立
模型求解
在假设的基础上,利用适当的数学工具来刻画各变量常量之间的数学关系,建立相应的数学结构。选择建模方法,由题目得到关系式,将目标转化为某一变量的函数。翻译一下:对变量和常量构建数学关系结构,得出函数。
利用获取的数据资料,对模型的所有参数做出计算(或者近似计算),推到模型的公式,将数学表达式变形为建模方法的标准形式,通过限制条件,对这个模型求解,此时可以用编程用数学软件进行计算。翻译一下:通过资料数据,利用自己建立的模型得出结果。
模型分析
对所要建立模型的思路进行阐述,对所得结果进行数学上的分析。包括误差分析,数据稳定性分析等等。翻译一下:这怎么翻译,就是单纯分析结果怎么样罢了。
模型检验
用非技术性的语言回答实际问题。将模型分析结果与实际情形进行比较,以此来验证模型的准确性,合理性和适用性。如果模型与实际较吻合,则要对计算结果给出其实际含义,并进行解释,如果误差较大需要修正模型。翻译一下:根据分析的结果查看模型是否符合要求。
备战
建模
掌握各类模型(功能,使用场景,需要条件,缺点或不足,哪里可以改进)
编程
Matlab或Python基础,可以实现各类常见的算法,对bug可以及时改正,能够利用编程软件制作图片
写作
能够掌握学术语言规范,明白论文各模块写作要求,能够对论文进行排版
赛题
预测类
根据已有的数据或现象找出其内在发展规律,然后对未来情形做预测的过程
小样本/大样本/小样本未来预测/大样本随机因素或周期特征的未来预测/大样本未来预测
步骤
- 确定预测目标
- 收集,分析资料
- 选择合适的预测方法进行预测
- 分析评价预测方法以及结果
- 修正预测结果
- 给出预测结果
方法
- 插值与拟合方法——小样本内部预测
- 回归分析发——中,大样本内部预测
- 灰色预测方法——小样本的未来预测(有固定趋势)
- 时间序列方法——中大样本的随机因素或周期特征的未来趋势未来预测
- 神经网络方法——大(特大)样本未来预测
评价类
按照一定的标准对事物的发展或者现状进行划分的过程在数学建模中题点可提现现在对生态环境,社会建设,方案策略等进行评价。一般没有明确指标体系和评价标准,往往需要查阅各类资料进行构建,所以一般没有明确答案。
要求
全面,准确,独立
步骤
- 明确评价目的
- 确定被评价对象
- 建立评价指标体系
- 确定指标对应的权重系数
- 选择或构造综合评价模型
- 计算各系统的综合评价值
- 给出综合评价结果
机理分析类(少见)
机理分析是根据对现实对象特性的认识,分析其因果关系,找出反映内部机理的规律。在求解机理分析类问题时首先需要探索与问题相关的物理,化学,经济等相关知识,然后通过对已知数据或现象的分析对事物的内在规律做出必要的假设,最后通过构建合适的方程或关系式对其内在的规律进行数值表达。
赛题
机理分析立足于建立事物内部的规律,相对于其他类型的赛题均有章可循,机理分析类赛题往往需要结合相关众多关联知识才能求解,如空气动力学,流体力学,热力学等。
优化类
在现有条件固定的情况下,如何使目标效果达到最佳。如在一座城市公交车公司拥有公交车数量固定的,问如何安排线路能够使盈利达到最高。优化类往往需要 三个关键因素:目标函数,决策变量,约束条件。
步骤
- 确定优化目标
- 确定决策变量
- 构建目标函数
- 根据已知条件构建约束条件
- 选择合适的方法求解目标函数
- 给出优化结果
线性规划
在人们的生产实践中,经常遇到如何利用现有资源来安排生产,以取得最大经济效益的问题。这类问题构成了运筹学的一个重要分支——数学规划,而线性规划则是数学规划的一个重要分支。
例题

解法

定义
目标函数及约束条件均为线性函数,故被称为线性规划问题。线性规划问题是在一组线性约束条件的限制下,求一线性函数最大或最小的问题。
在解决实际问题时候,把问题归结成一个线性规划数学模型是很重要的一步,往往也是很困难的一步,模型建立是否恰当,直接影响到求解。而选适当的决策变量是我们建立有效模型的关键之一。
matlab的线性规划求法:
线性规划的目标函数可以是求最大值也可以是求最小值,约束条件的不等号可以是小于号也可以是大于号。为了避免这种形式多样性带来的不便。Matlab中规定线性规划的标准形式为:
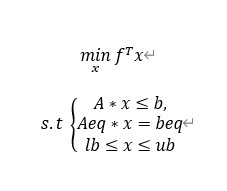
式中:
f,x,b,beq,lb,ub为列向量,其中 f 称为价值向量,b称为资源向量, A,Aeq为矩阵。
MATLAB中求解线性规划的命令为:
[x,fval]=linprog(f,A,b);
[x,fval]=linprog(f,A,b,Aeq,beq);
[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub);
[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub,x0,OPTIONS);
[x,fval]=linprog(----);
[x,fval,exitflag,output]=linprog(----);
[x,fval,exitflag,output,lambda]=linprog(----);- x返回决策向量的取值,即最优值;
- fval返回目标函数的最优值;
- A和b对应线性不等式约束;
- Aeq和beq对应线性等式约束;
- lb和ub分别对应决策向量的下界向量和上界向量;
- x0是x的初始值;OPTIONS是控制参数,为指定参数进行最小化;
- exitflag表示收敛数;output表示迭代次数;
例题
题目
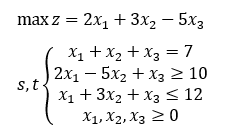
求解
先化成matlab线性规划标准型,即
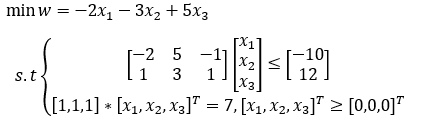
代码如下
f=[-2;-3;5];
a=[-2,5,-1;1,3,1];
b=[-10;12];
aeq=[1,1,1];
beq=7;
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1));
x
y=-y %%注意此处,由于前面将函数取反来求最优值,所以这里要把反的转化为正的
可行解
满足约束条件的解x=【x1,L,xn】T,称为线性规划问题的可行解,而使目标函数达到最大值的可行解成为最优解。
可行域
所有可行解构成的集合成为问题的可行域,记为R。
案例

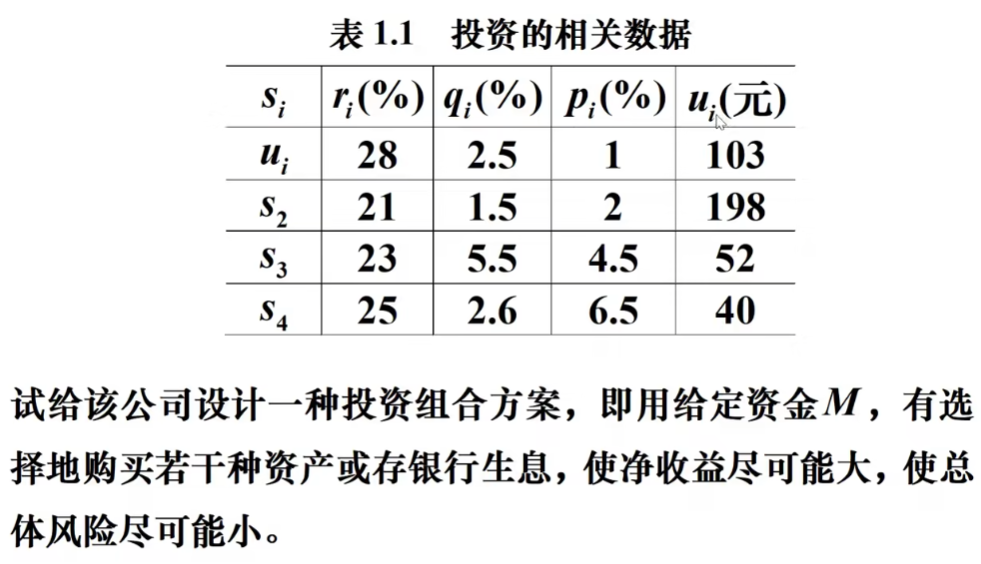
(ui处应该是S1)
作业
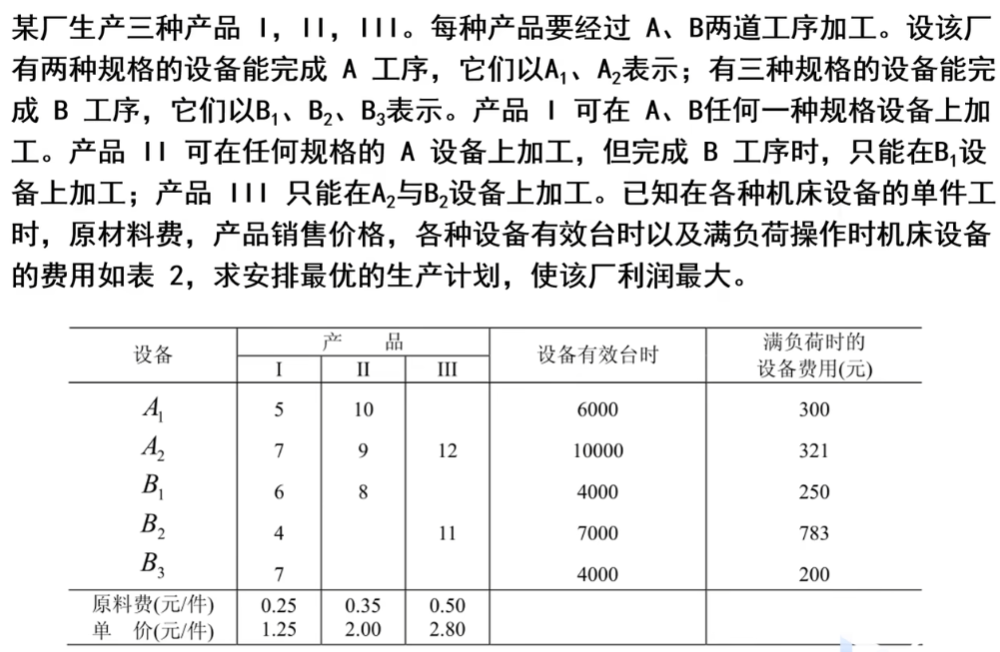
整数规划
数学规划中的变量(部分或全部)限制为整数时,称为整数规划。如果在线性规划模型中,变量限制为整数,则称为整数线性规划。目前流行求解整数规划的方法往往只适用于整数线性规划,还没有方法能够有效求解一切整数规划。
matlab中
线性规划[x,fval] = linprog[c,A,b,aeq,beq,lb,ub,x0]
整数规划[x,faval] = intlinprog[c,intcon,A,b,aeq,beq,lb,ub]【intcon为整数所在位置】
其中整数规划代码可以解决指派问题以及0-1规划
其中intcon若为[1,2,3]则表示第一个第二个第三个决策向量为整数
若intcon为[2,3]则表示第二个第三个决策向量为整数
也就是说第几个为决策向量就顺序填几
分类
- 线性整数规划:可以直接用matlab求解
- 非线性整数规划:无特定算法,只能够用近似算法,如蒙特卡洛模拟,智能算法
- 0-1规划:特殊的整数规划,matlab中只能做到线性0-1规划,非线性0-1规划只能求近似求解
整数规划和线性规划的关系
整数规划的可行解是松弛问题可行域中的整数格点
松弛问题指的是删去约束条件
松弛问题无可行解,则整数规划无可行解
松弛问题最优解满足整数要求,则该最优解为整数规划最优解

特点
- 原线性规划有最优解,当变量限制为整数后会出现下述情况
1.原线性规划最优解全是整数,整数规划最优解和线性规划最优解一致
2.整数规划无可行解
3.有可行解(当然存在最优解),但是优解值变差 - 整数规划最优解不能按照实数最优解简单取解而获得
求解方法
从数学模型上看整数规划似乎是线性规划的一中特殊形式,求解只需要在线性规划的基础上舍入求解,寻求满足整数要求的解就行
但是实际上两者有很大的不同,通过舍入得到的解也不一定就是最优解,有时候还不能保证所得到的解是整数可行解
- 分枝定界法——可求纯或混合整数线性规划
- 割平面法——可求纯或混合整数线性规划
- 隐枚举法——求解“0-1”整数规划:
1.过滤隐枚举法
2.分枝隐枚举法 - 匈牙利法——解决指派问题(“0-1”规划特殊情况)
- 蒙特卡洛法——求解各类型规划
分枝定界法
对有约束条件的优化问题(其可行解为有限数)的所有可行解空间恰当地进行系统搜索,这就是分枝与定界内容。通常,把全部可行解空间反复地分割为越来越小的子集,称为分枝;并且对每个子集内的解集计算一个目标下界(对于最小值问题),这称为定界。在每次分枝后,凡是界限超出已知可行解集目标值的那些子集不再进一步分枝,这样,许多子集可不予考虑,这称剪枝。这就是分枝定界法的主要思路。
分枝定界法可用于解纯整数或混合的整数规划问题。在本世纪六十年代初由 Land Doig 和 Dakin 等人提出的。由于这方法灵活且便于用计算机求解,所以现在它已是解整数规划的重要方法。目前已成功地应用于求解生产进度问题、旅行推销员问题、工厂选址问题、背包问题及分配问题等。
求解整数规划
首先求非整数约束最优解,如果是整数解则直接作为整数规划最优解
如果不是整数解则需要选某个整数变量分支
添加约束(一般为非整数约束时最优解的下整数为下界,上整数为上界)作为新的条件
再次求解,看解是否是整数,若为整数则直接作为整数规划最优解
如果不是整数则需要再次循环以上步骤
直到求出最优解
割平面法
- 如果松弛问题无解,那么整数规划也无解
- 如果松弛问题的解为整数解则也是整数规划的解
- 如果松弛问题含有非整数分类,则对松弛问题增加割面条件,即加上线性约束(擦掉非最优可行解)

吐槽
整数规划在matlab的intlinprog基本可以概览求解,所以后面的方法就不细细学了
而且每种方法是真的复杂啊我靠,学不下去了要。。。
蒙特卡洛模拟
暴力求解()是一种随机模拟
名字来源于法国南方的一个赌博圣地国家。
层次分析法
笔记来源:点我QAQ
指标选择途径
题目背景
- 中国知网,百度学术等搜索文献
- 网站推荐:虫部落https://search.chongbuluo.com/
- 其他途径:谷歌搜索,微信搜索,知乎搜索
要求:一定要有依据,并且说明这些指标以及指标所代表的含义
介绍
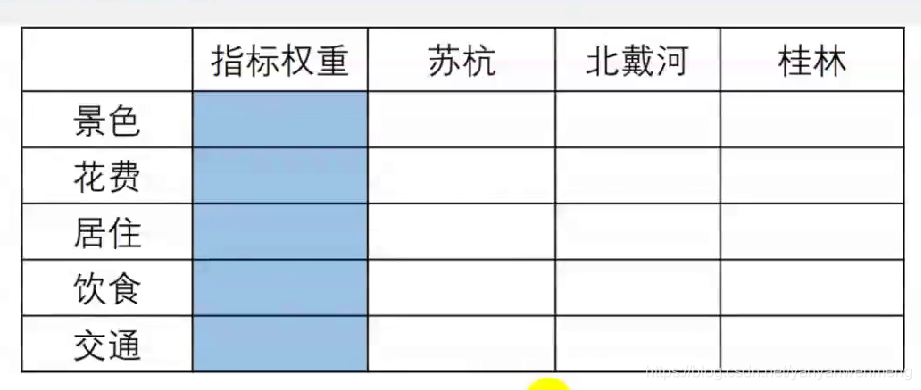
比如要确定景色、花费等五个指标的权重,该如何确定呢?
如果一次性考虑五个指标的关系,往往考虑不周
【解决办法】两个两个指标之间进行比较,最终根据两两比较的结果来推算出权重。——层次分析法的思想
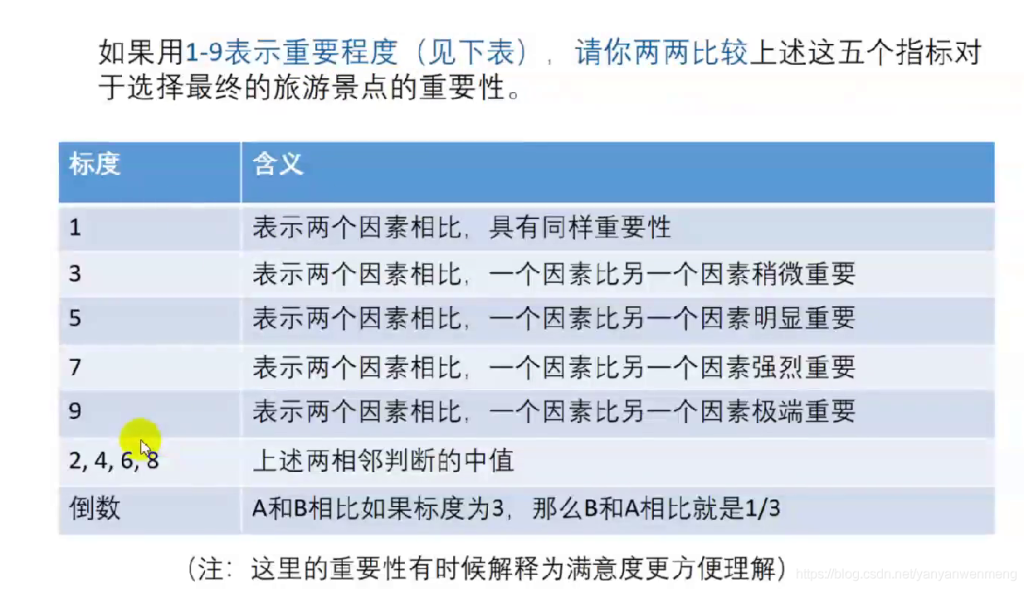
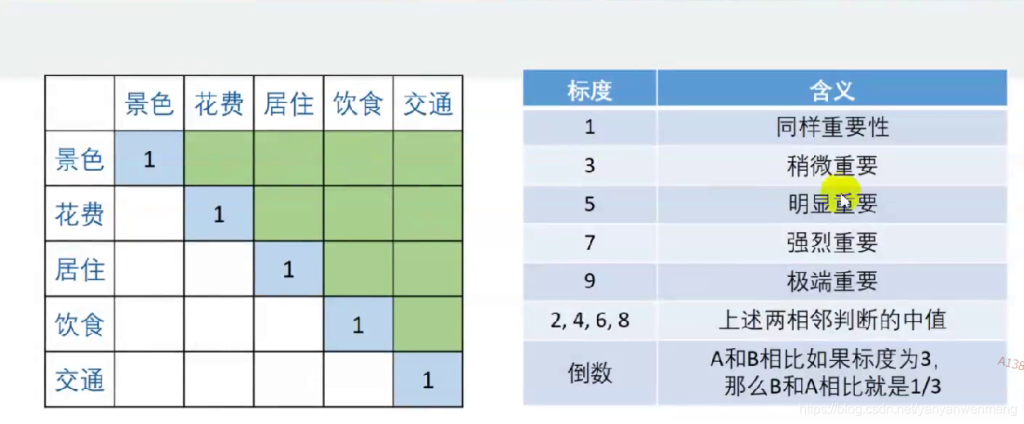
比如如果花费比景色略微重要,则花费和景色交际处填2,且对应aij与aji应该互为倒数!!!
最后得到所有图表
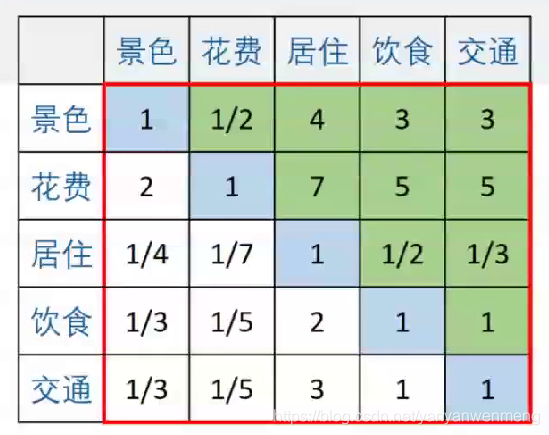
该判断矩阵实际需要专家填写
矩阵不一致问题
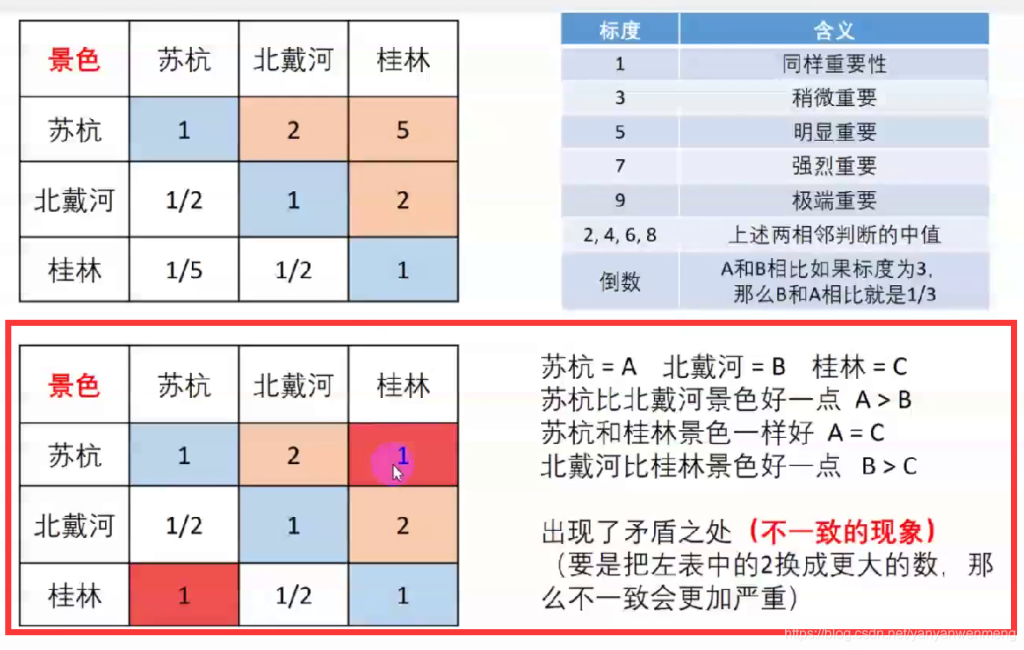
如上图就出现了比较的一个错误现象
一致矩阵的满足条件

如图
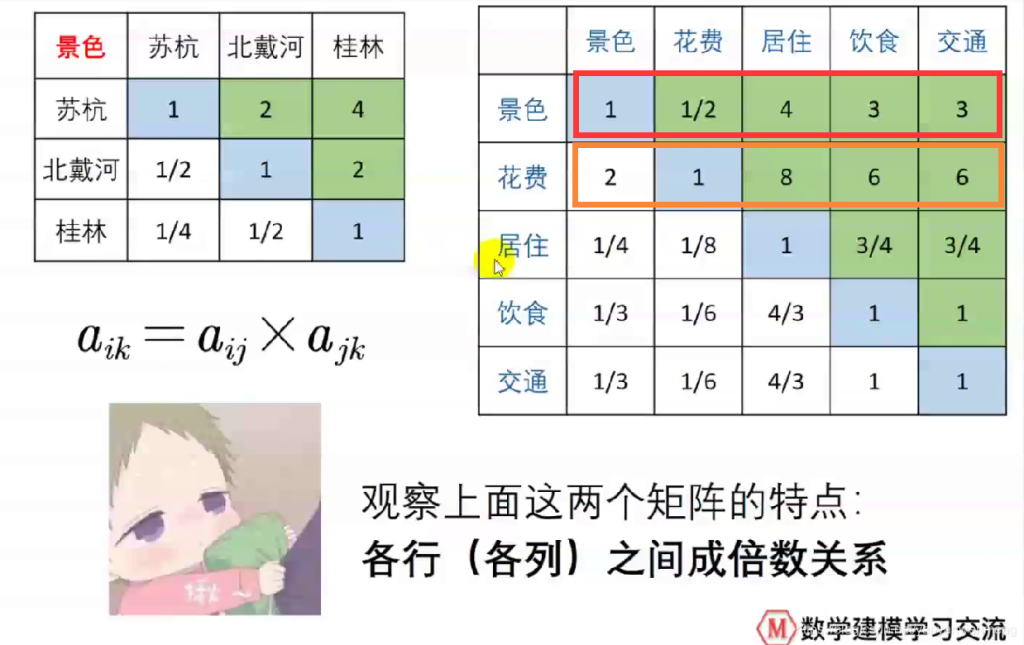
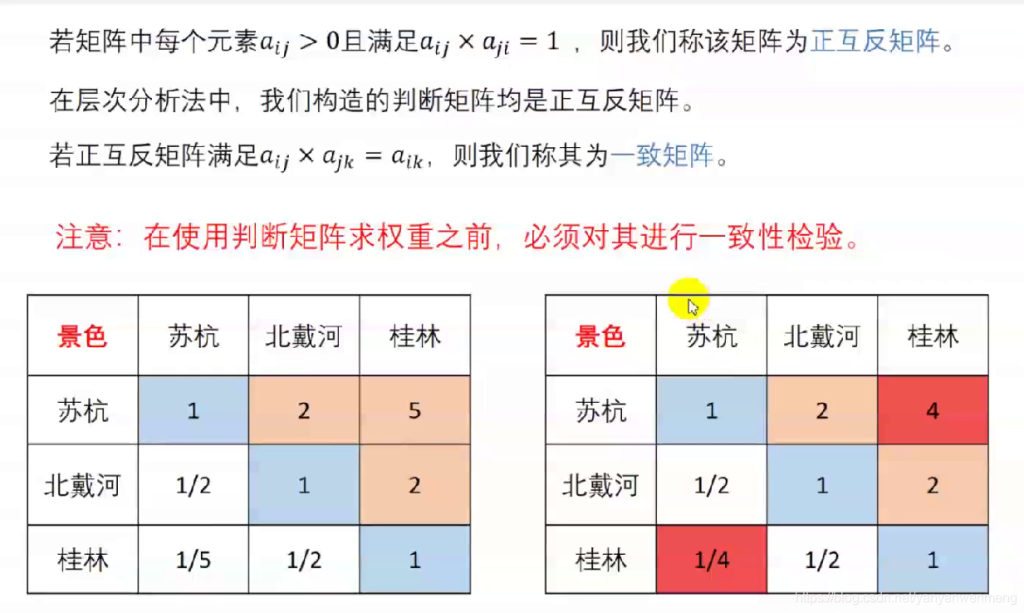
并非;一定要绝对一致矩阵,但是一致性不能偏差太大
一致性检验
【原理】检验我们构造的判断矩阵和一致矩阵是否有太大的差别。

黄色框表示第2、3……n行的值和第一行成倍数关系(也可以定义为列与列之间成比例)。

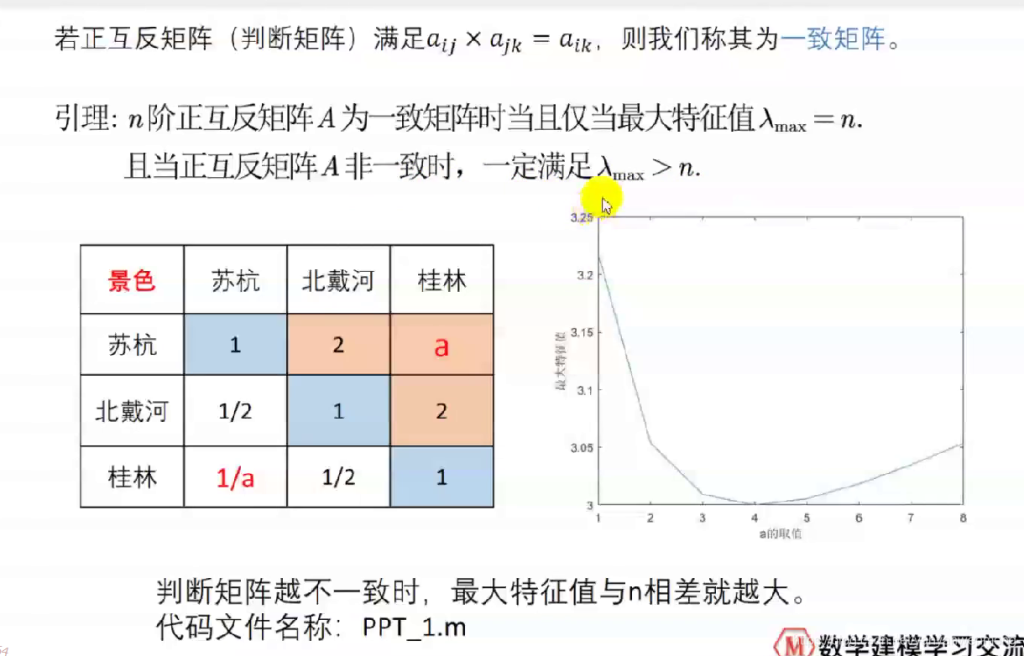
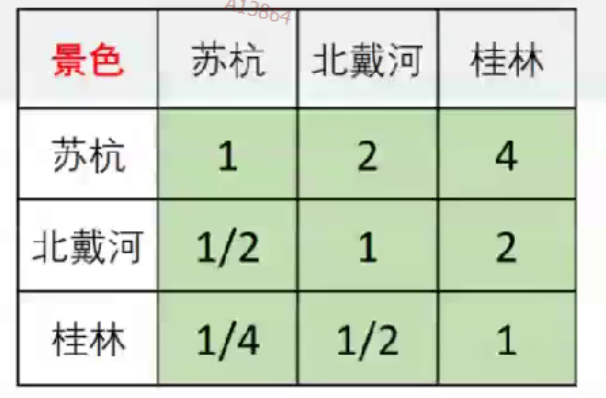
求上表格的最大特征值matlab代码如下
A = [1 2 4; 1/2 1 2; 1/4 1/2 1];
eig(A)%求每一行的特征值,共有3个
发现最大特征值为3
如果矩阵不一致,会出现最大特征值大于3
也就是说最大特征值>n(n阶矩阵),且判断矩阵越不一致,最大特征值与n相差就越大
一致性检验步骤
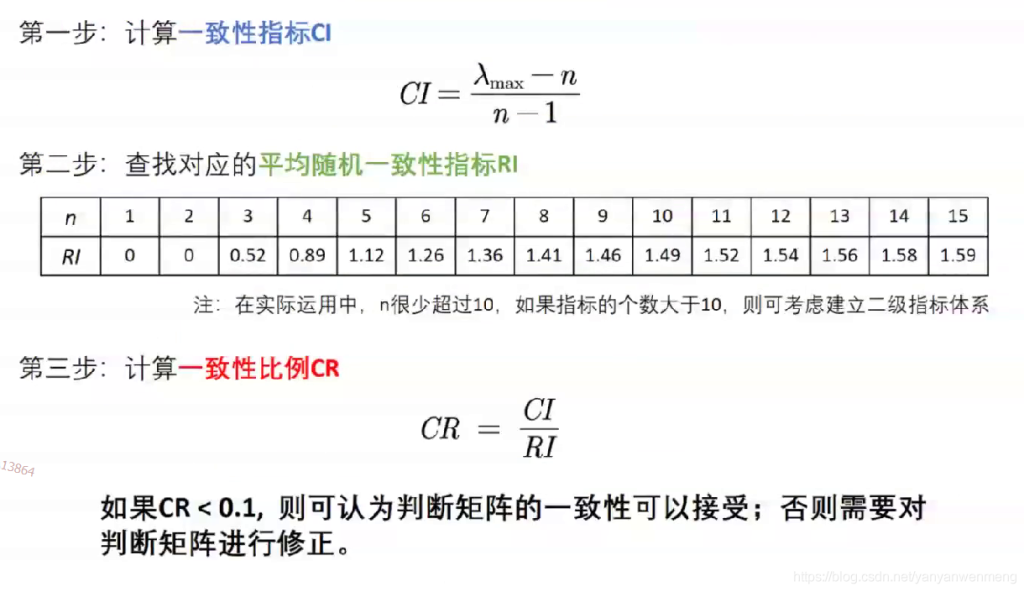

【注意】当一致性检验通过后才可计算权重,如果一致性检验通不过,则需要重新调整判断矩阵。
权重计算
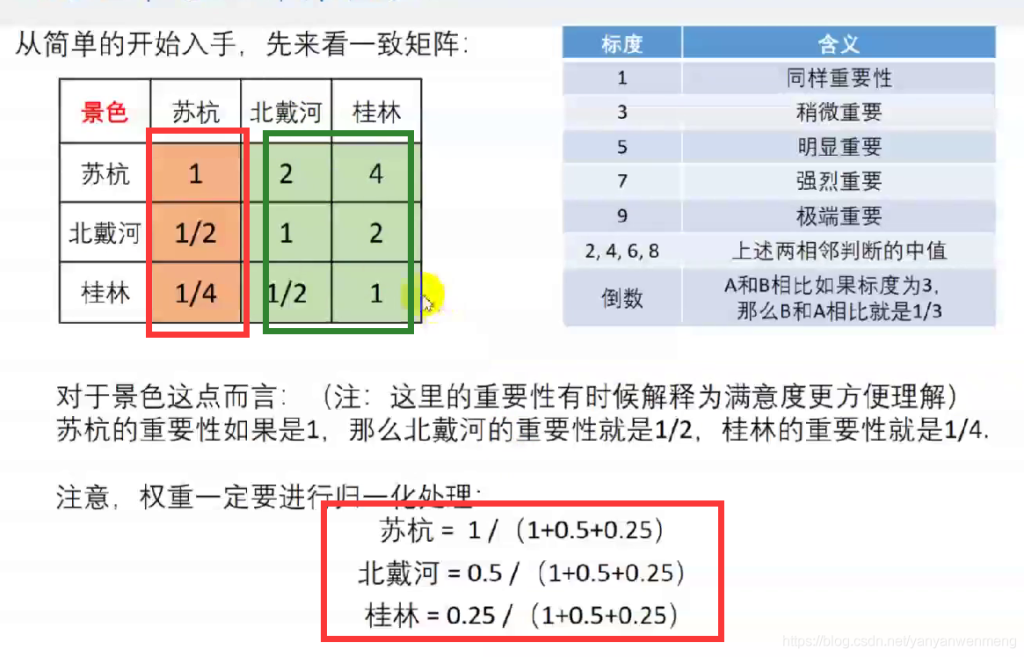
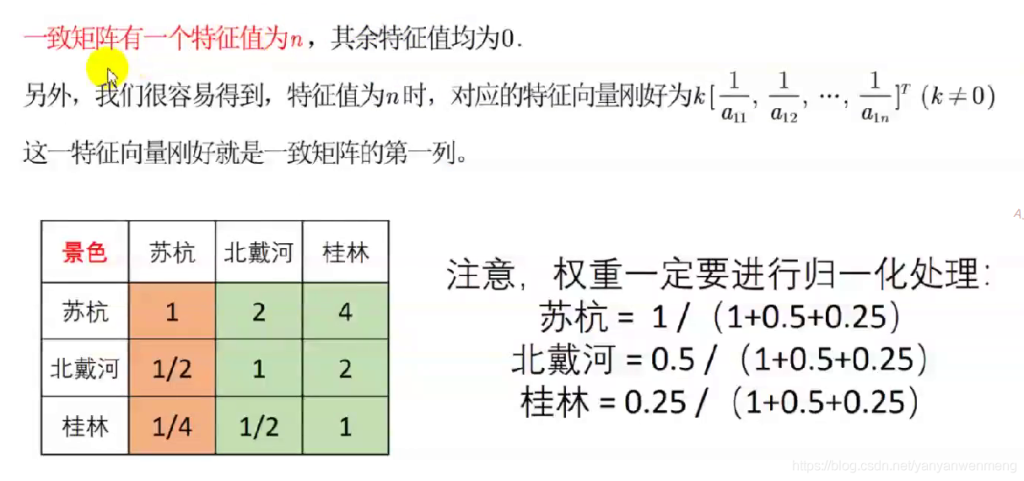
也可以按照第二列或者第三列的数据进行计算。权重计算完后需要归一化处理。
由于判断矩阵不一定为一致矩阵,所以它的各行(列)之间不一定成比例,因此,计算权重时需要利用每一列的数据把权重计算出来,最后利用三种方法求权重即可。
比如下面这个判断矩阵(不是一致矩阵,因为各行不成比例)
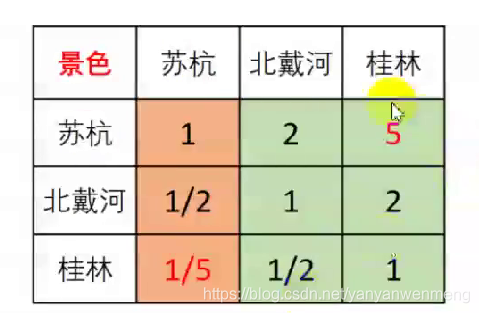
计算出每一列的权重:
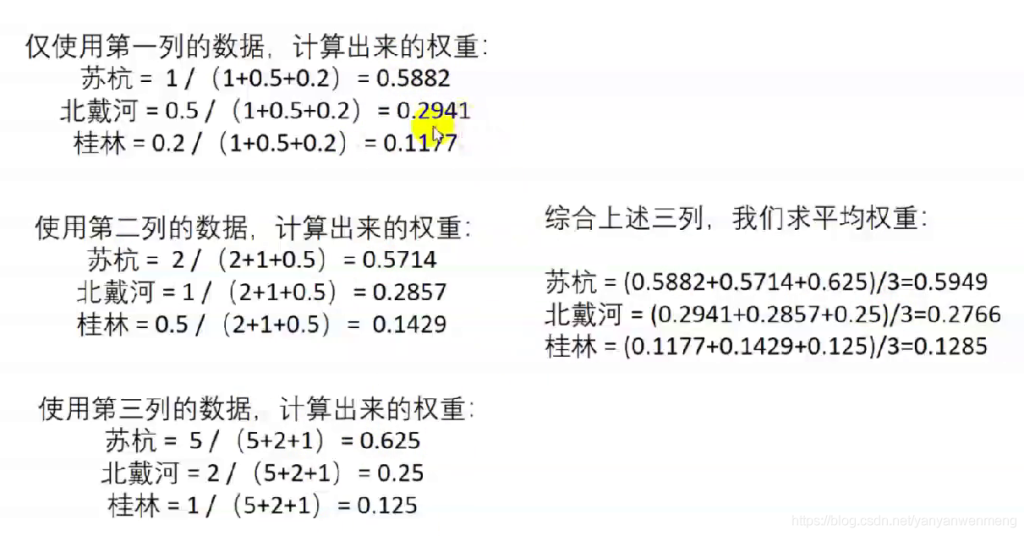
算术平均法求权重
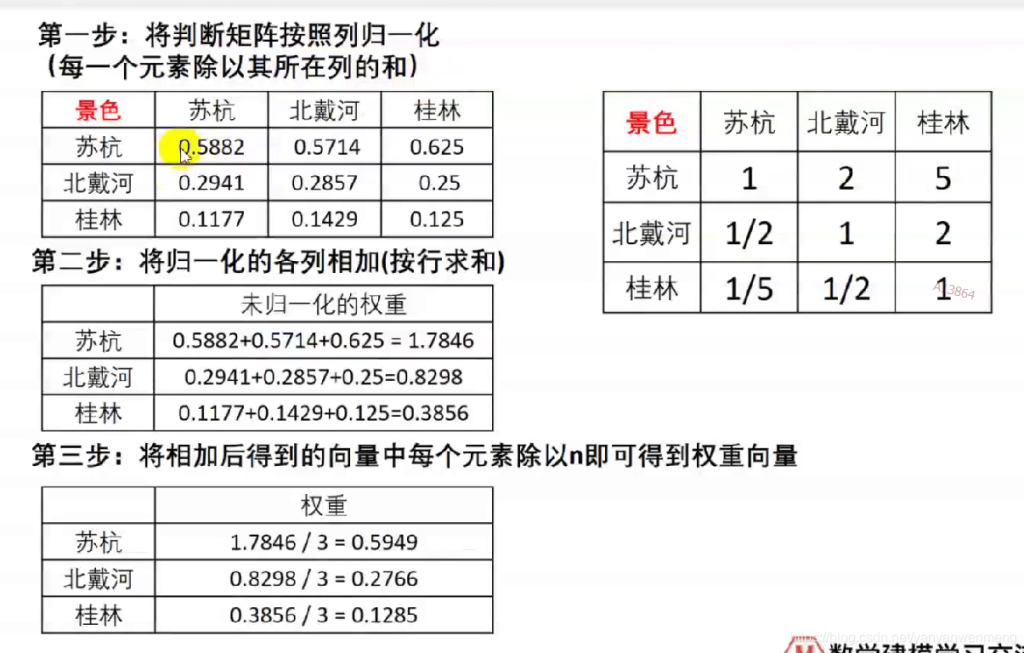
数学公式:

几何平均法求权重
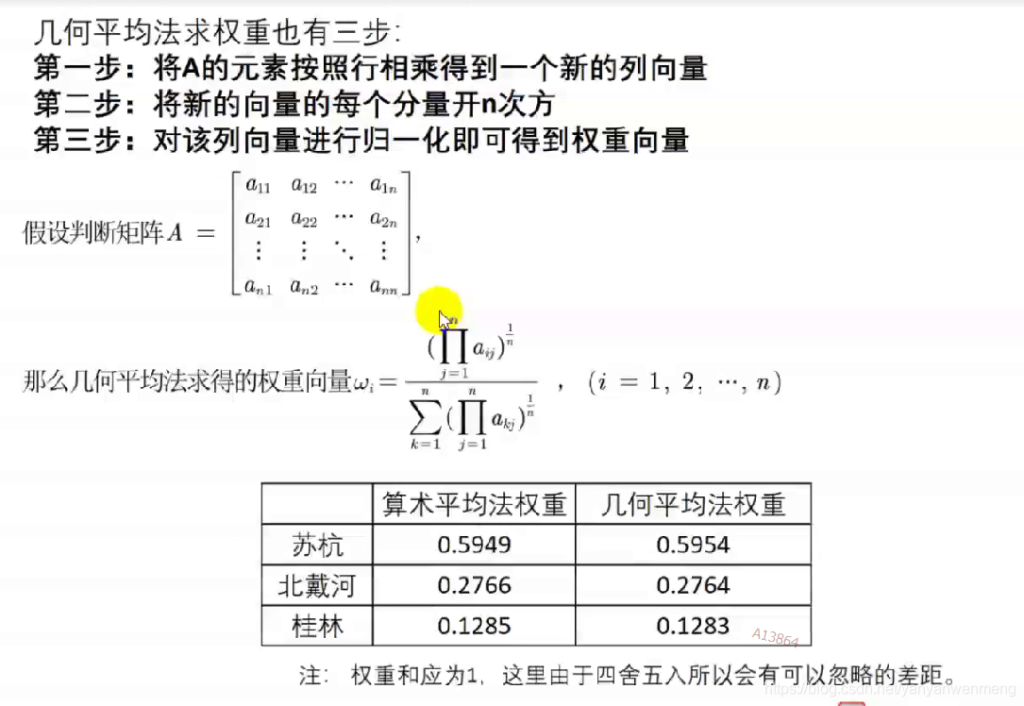
几何平均法求权重也有三步:
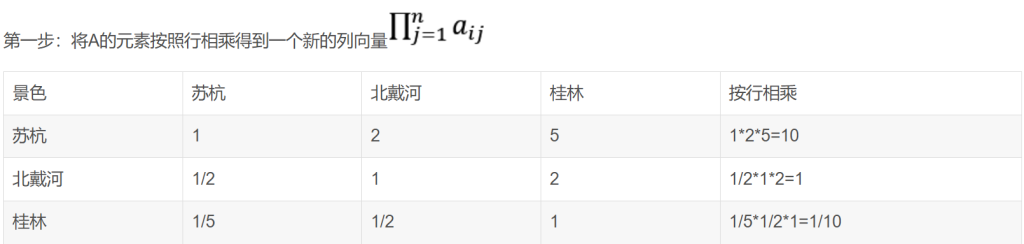

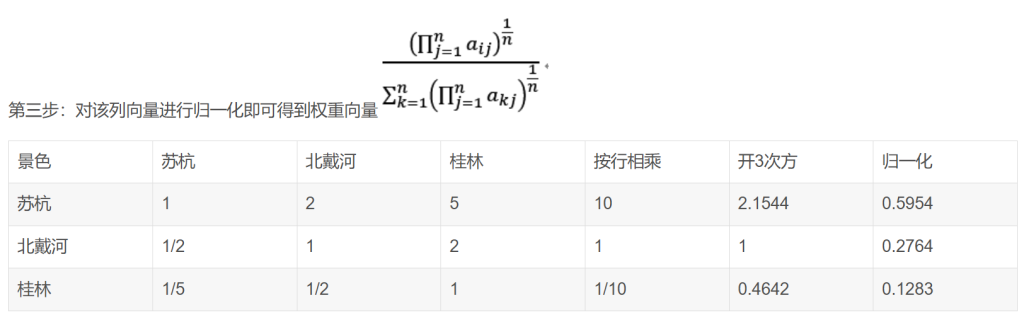
特征值法求权重(用的最多,建议使用这个)
判断矩阵求权重
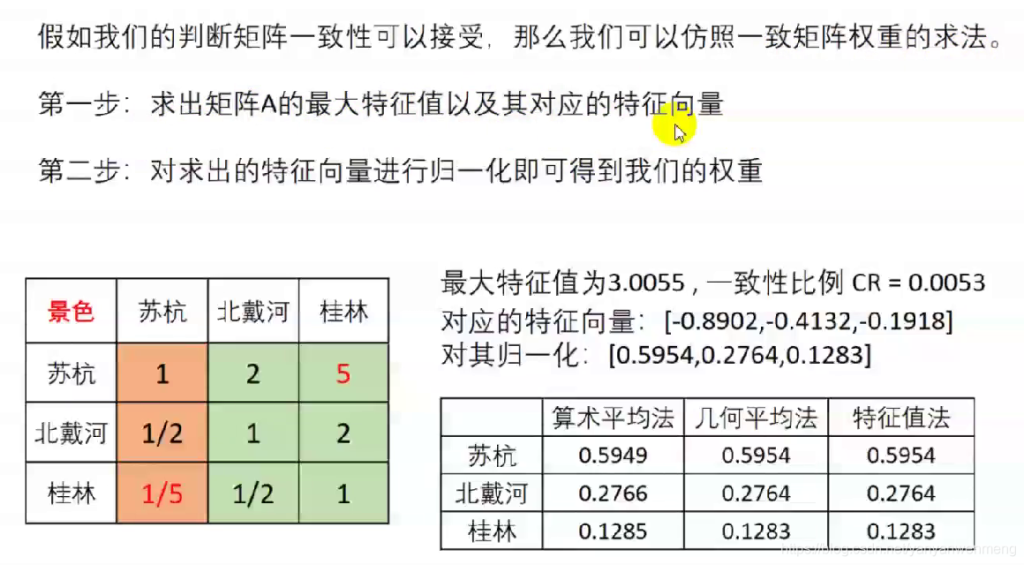
matlab求解:
A = [1 2 5; 1/2 1 2; 1/5 1/2 1];
[V D] = eig(A)

最大特征值为3.0055,对应的特征向量为[-0.8902 -0.4132 -0.1918]
CI = (3.0055-3)/2
CR = CI/0.52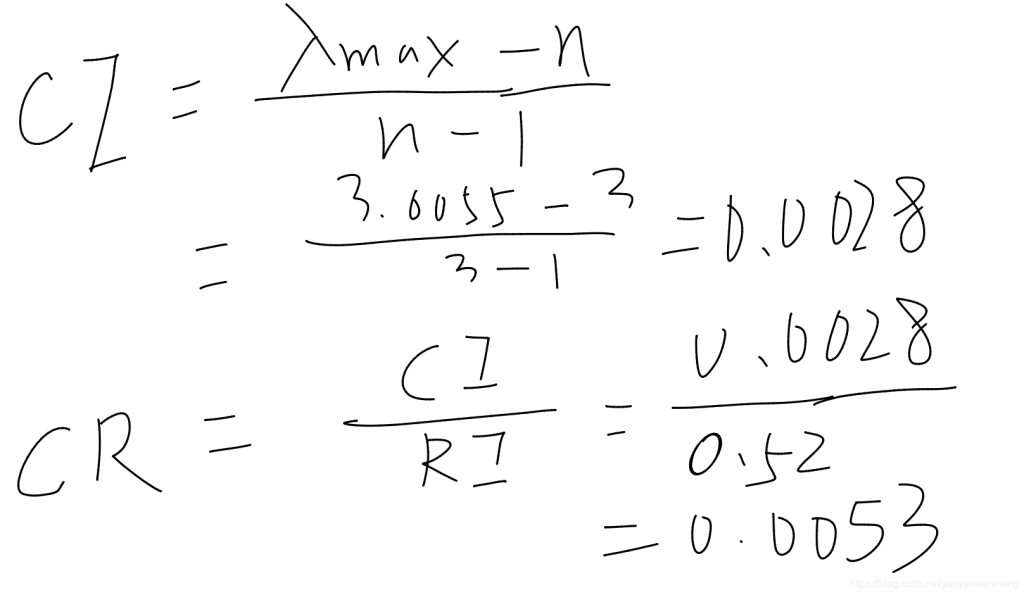
CR = 0.0053 < 0.1 ,说明此矩阵的一致性可以接受。
求权重:
V = [-0.8902 -0.4132 -0.1918]
S = sum(V)
G = [V(1,1)/S V(1,2)/S V(1,3)/S]%归一化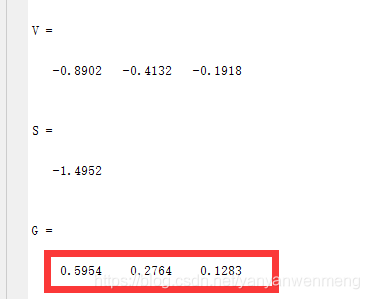
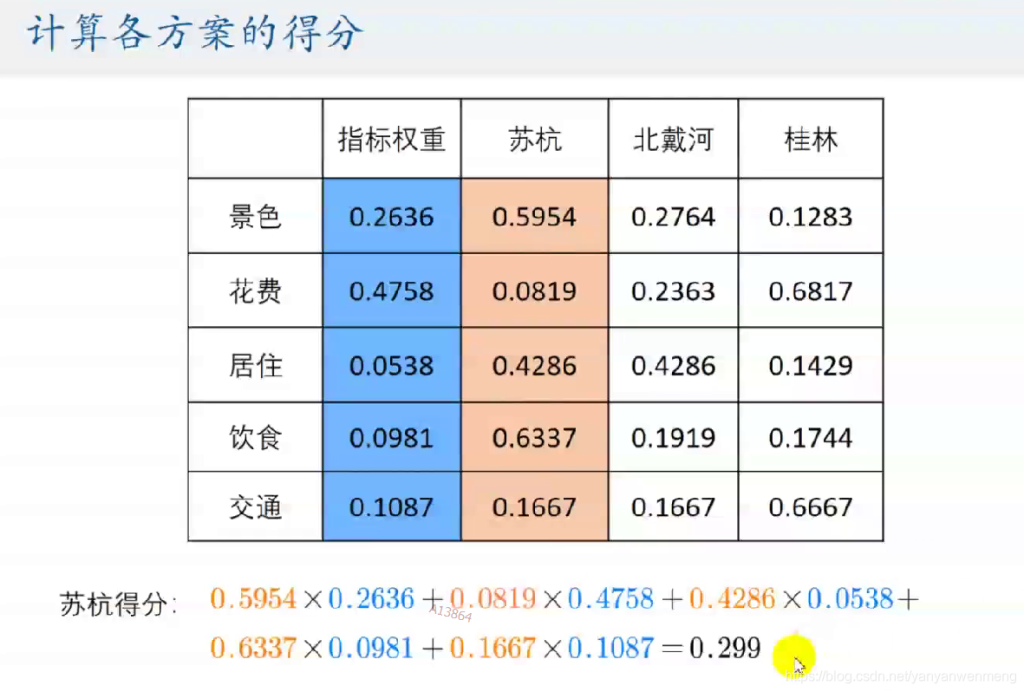
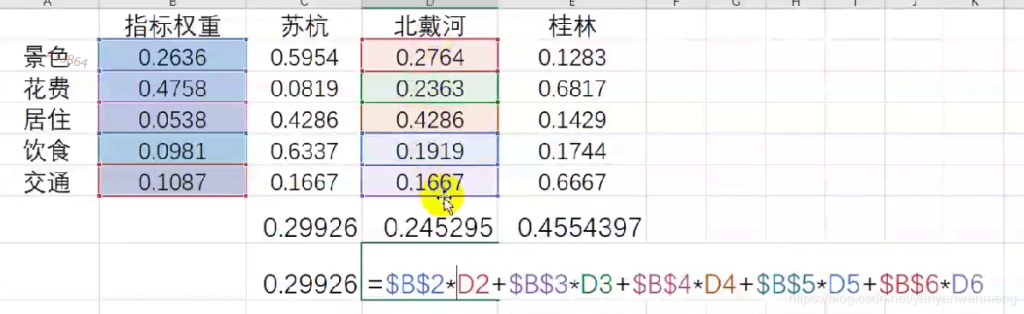
excel中进行计算每个城市的得分(需要用“$”符号锁定单元格):
求权重matlab代码
%% 注意:在论文写作中,应该先对判断矩阵进行一致性检验,然后再计算权重,因为只有判断矩阵通过了一致性检验,其权重才是有意义的。
%% 在下面的代码中,我们先计算了权重,然后再进行了一致性检验,这是为了顺应计算过程,事实上在逻辑上是说不过去的。
%% 因此大家自己写论文中如果用到了层次分析法,一定要先对判断矩阵进行一致性检验。
%% 而且要说明的是,只有非一致矩阵的判断矩阵才需要进行一致性检验。
%% 如果你的判断矩阵本身就是一个一致矩阵,那么就没有必要进行一致性检验。
disp('请输入判断矩阵A')
A=input('A=');
[n,n] = size(A);
% % % % % % % % % % % % %方法1: 算术平均法求权重% % % % % % % % % % % % %
Sum_A = sum(A);
SUM_A = repmat(Sum_A,n,1);
Stand_A = A ./ SUM_A;
disp('算术平均法求权重的结果为:');
disp(sum(Stand_A,2)./n)
% % % % % % % % % % % % %方法2: 几何平均法求权重% % % % % % % % % % % % %
Prduct_A = prod(A,2);
Prduct_n_A = Prduct_A .^ (1/n);
disp('几何平均法求权重的结果为:');
disp(Prduct_n_A ./ sum(Prduct_n_A))
% % % % % % % % % % % % %方法3: 特征值法求权重% % % % % % % % % % % % %
[V,D] = eig(A);
Max_eig = max(max(D));%求最大特征值
[r,c]=find(D == Max_eig , 1);
disp('特征值法求权重的结果为:');
disp( V(:,c) ./ sum(V(:,c)) )
% % % % % % % % % % % % %下面是计算一致性比例CR的环节% % % % % % % % % % % % %
CI = (Max_eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦,这里的RI最多支持 n = 15
% 这里n=2时,一定是一致矩阵,所以CI = 0,我们为了避免分母为0,将这里的第二个元素改为了很接近0的正数
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因为CR<0.10,所以该判断矩阵A的一致性可以接受!');
else
disp('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!');
end特征值求法权重:要保证矩阵是逆矩阵
%% 输入判断矩阵
clear;clc
disp('请输入判断矩阵A: ')
% A = input('判断矩阵A=')
A =[1 1 4 1/3 3;
1 1 4 1/3 3;
1/4 1/4 1 1/3 1/2;
3 3 3 1 3;
1/3 1/3 2 1/3 1]
% matlab矩阵有两种写法,可以直接写到一行:
% [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 两行之间以分号结尾(最后一行的分号可加可不加),同行元素之间以空格(或者逗号)分开。
[n,n] = size(A) % 也可以写成n = size(A,1)
%% 方法3:特征值法求权重
% 第一步:求出矩阵A的最大特征值以及其对应的特征向量
[V,D] = eig(A) %V是特征向量, D是由特征值构成的对角矩阵(除了对角线元素外,其余位置元素全为0)
Max_eig = max(max(D)) %也可以写成max(D(:))哦~ 求最大特征值
% 那么怎么找到最大特征值所在的位置了? 需要用到find函数,它可以用来返回向量或者矩阵中不为0的元素的位置索引。
% 那么问题来了,我们要得到最大特征值的位置,就需要将包含所有特征值的这个对角矩阵D中,不等于最大特征值的位置全变为0
% 这时候可以用到矩阵与常数的大小判断运算
D == Max_eig
[r,c] = find(D == Max_eig , 1)
% 找到D中第一个与最大特征值相等的元素的位置,记录它的行和列。
% 第二步:对求出的特征向量进行归一化即可得到我们的权重
V(:,c)%未归一化的结果
disp('特征值法求权重的结果为:');
disp( V(:,c) ./ sum(V(:,c)) )
% 我们先根据上面找到的最大特征值的列数c找到对应的特征向量,然后再进行标准化。
%% 计算一致性比例CR
CI = (Max_eig - n) / (n-1);
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦,这里的RI最多支持 n = 15
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因为CR < 0.10,所以该判断矩阵A的一致性可以接受!');
else
disp('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!');
end
评价类问题需要注意的细节
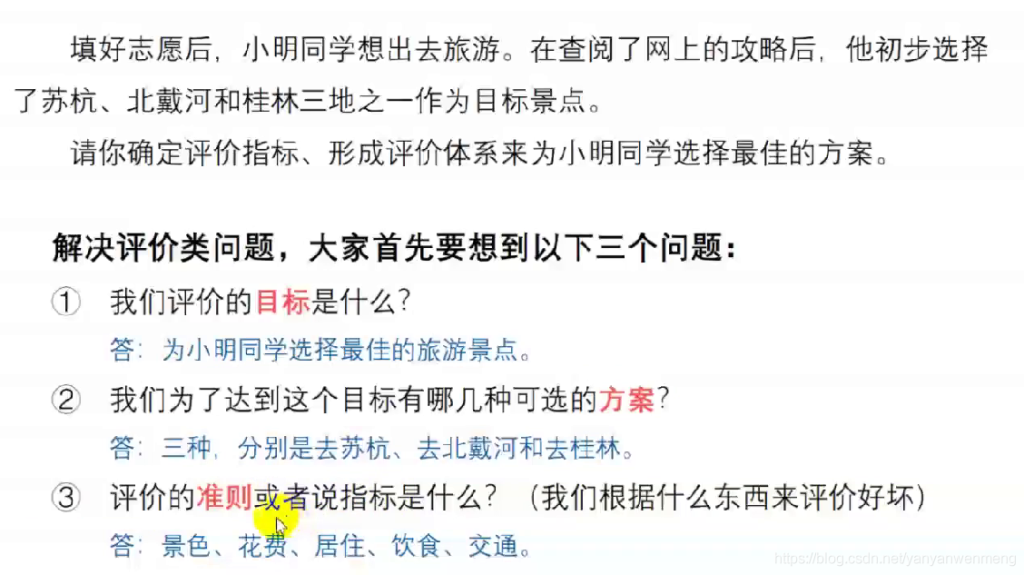
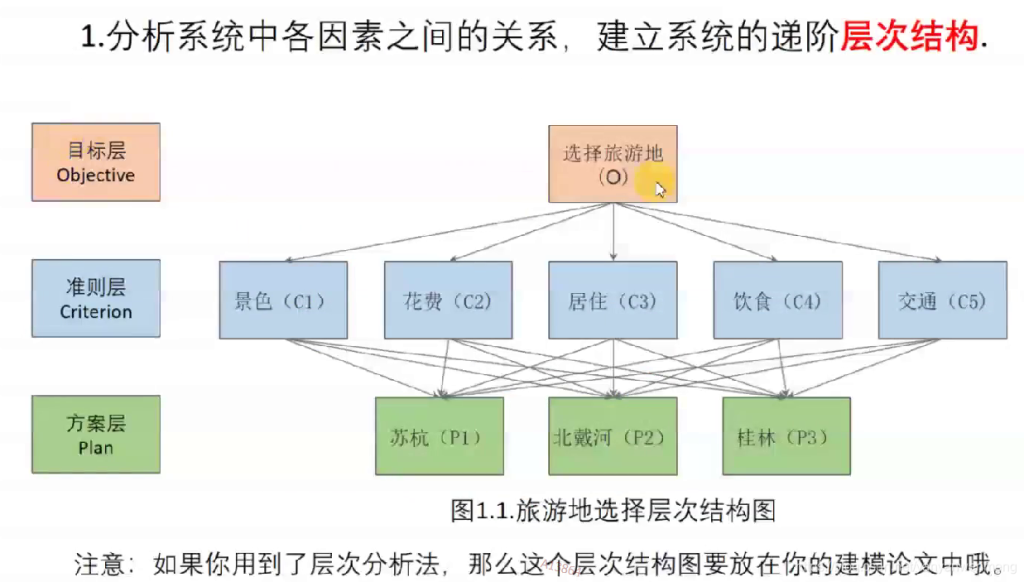
拓展模型
准则层可以有多层
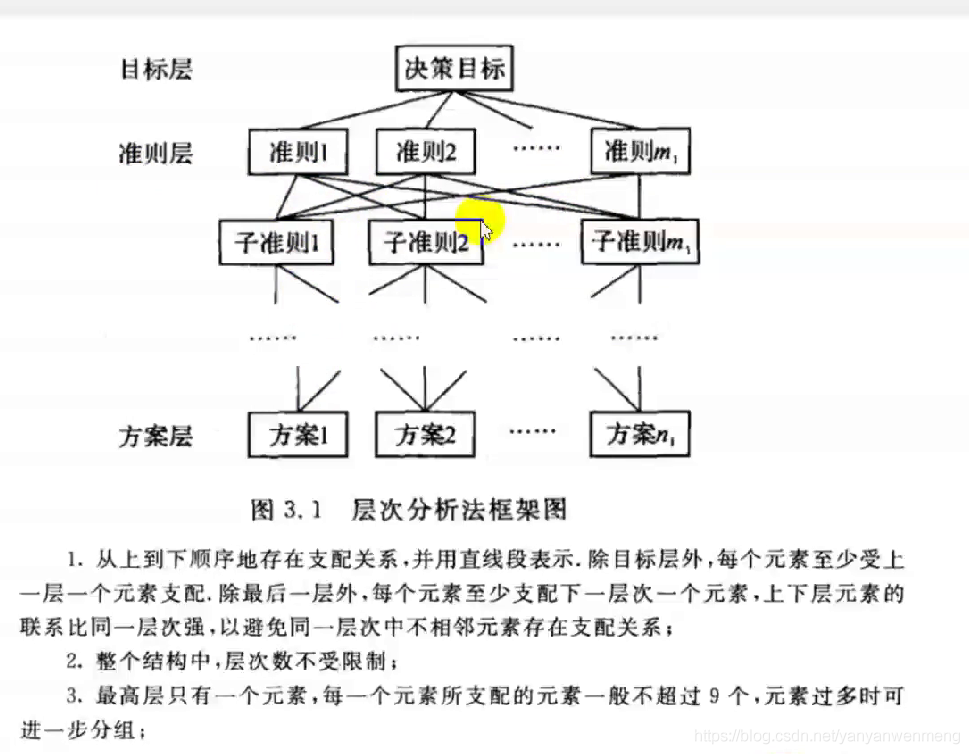
准则层不一定对应全部方案。比如:可以为一对二,如下图所示
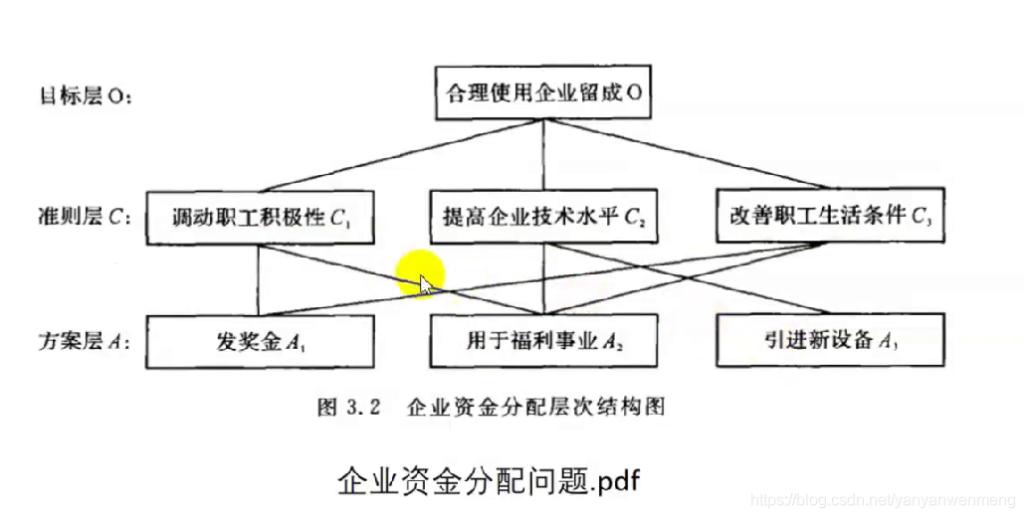
准则层不一定对应全部方案。比如:可以为一对一,如下图所示。
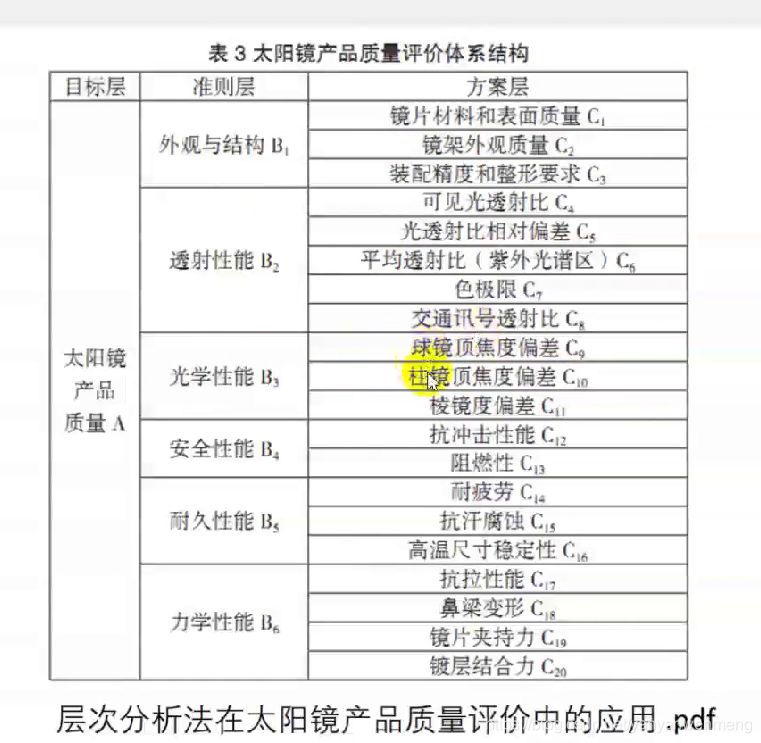
备注
使用层次分析法的话,层次结构图一定一定一定要画出来!!!

模糊综合评判
以下笔记来源于MATLAB实现模糊综合评判CSDN博客
模糊综合评判法
模糊综合评价法是一种基于模糊数学(fuzzy mathematics)的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
在司守奎《数学建模算法与应用》(第2版)一书的14.2节,介绍了将该方法用于多目标决策的过程,实现了在人事考核中运用模糊综合评判。下文中的数据和步骤都基于此书的内容,重点在于代码。
一级模糊综合评判的步骤
一级评判的运算较为简单,没有专门的程序,重在理解其思路
(1)确定因素集。对员工的表现,需要从多个方面进行综合评判,如员工的工作业绩、工作态度、沟通能力、政治表现等。所有这些因素构成了评价指标体系集合,即因素集,记为
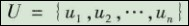
(2)确定评语集。由于每个指标的评价值的不同,往往会形成不同的等级。如对工作业绩的评价有好、较好、中等、较差、很差等。由各种不同决断构成的集合称为评语集,记为
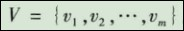
(3)确定各因素的权重。一般情况下,因素集中的各因素在综合评价中所起的作用是不相同的,综合评价结果不仅与各因素的评价有关,而且在很大程度上还依赖于各因素对综合评价所起的作用,这就需要确定一个各因素之间的权重分配,它是U上的一个模糊向量,记为
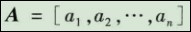
其中,所有a的和为1。
权重的确定方法很多,在实际运用中常用的方法有:Delphi法、专家调查法和层次分析法。
这一步往往是影响最终结果的重要原因。
(4)确定模糊综合判断矩阵。对n个指标来说,每个指标都有m个评语等级,构成n*m的矩阵R,R是一个从U到V的模糊关系矩阵。

(5)综合评判。如果有一个从U到V的模糊关系R,那么利用R就可以得到一个模糊变换
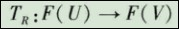
由此变换,就可以得到综合评判结果B = A·R。综合后的评判可以看作是V上的模糊向量,记为
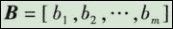
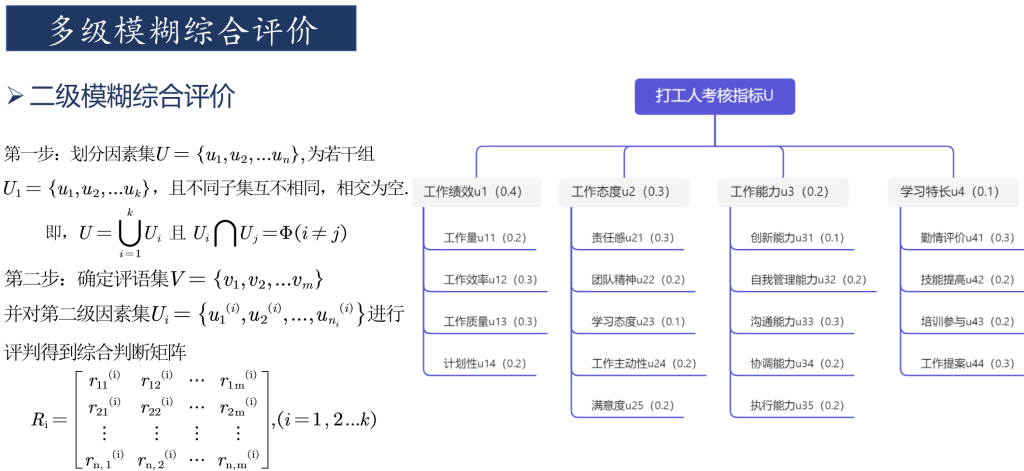
多层级模糊综合评判
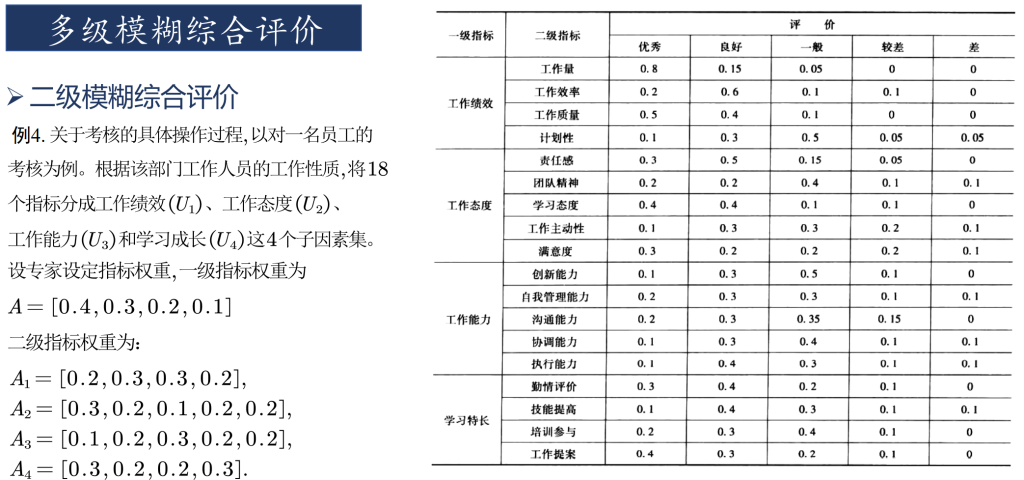
对于一些复杂的系统,如人事考核中涉及的指标较多时,需要考虑的因素很多,这时如果仍用一级模糊综合评判,则会出现两个方面的问题:一是因素过多,它们的权数分配难以确定;另一方面,即使确定了权分配,由于需要满足归一化条件,每个因素的权值都小,对这种系统,可以采用多层次模糊综合评判方法。对于人事考核而言,采用二级系统就足以解决问题了,如果实际中要划分更多的层次,那么可以用二级模糊综合评判的方法类推。
实现的思路是将每一个原指标作为一级指标,划分出二级指标,从而可以对一级指标进行评判。然后根据结果再进行一次评判。
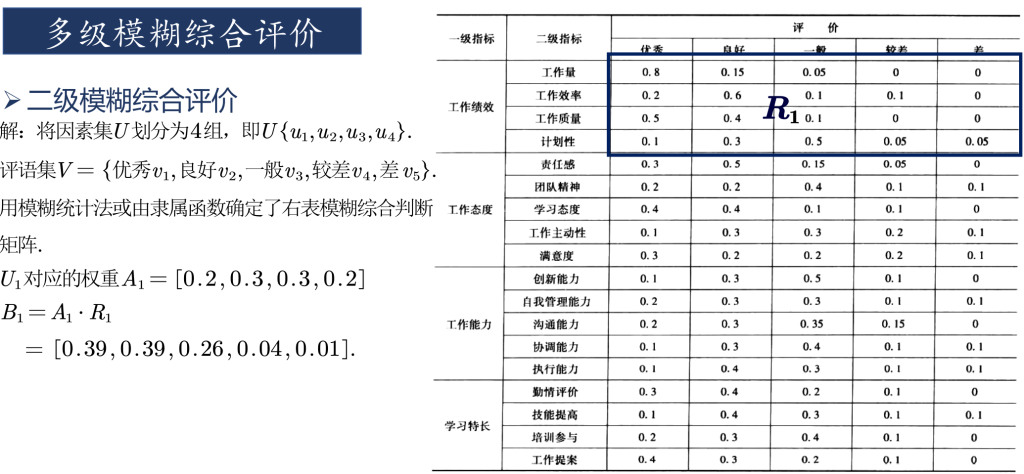
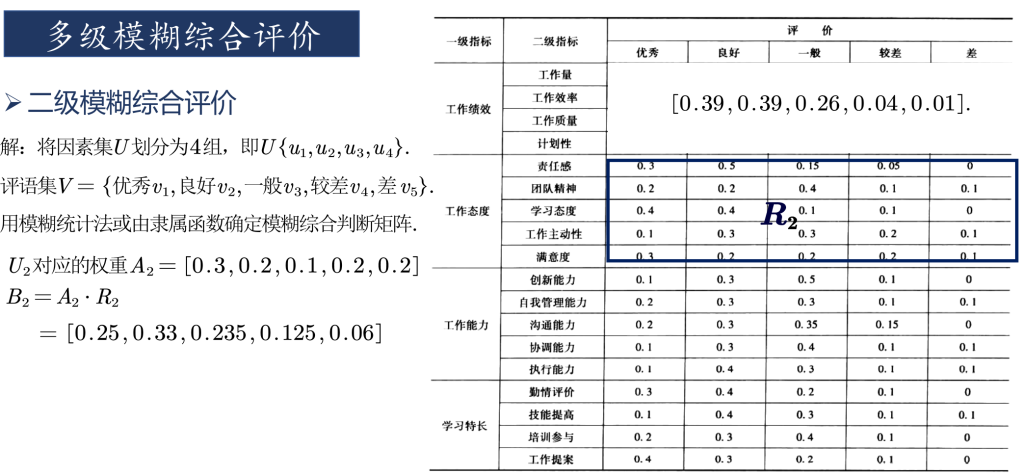
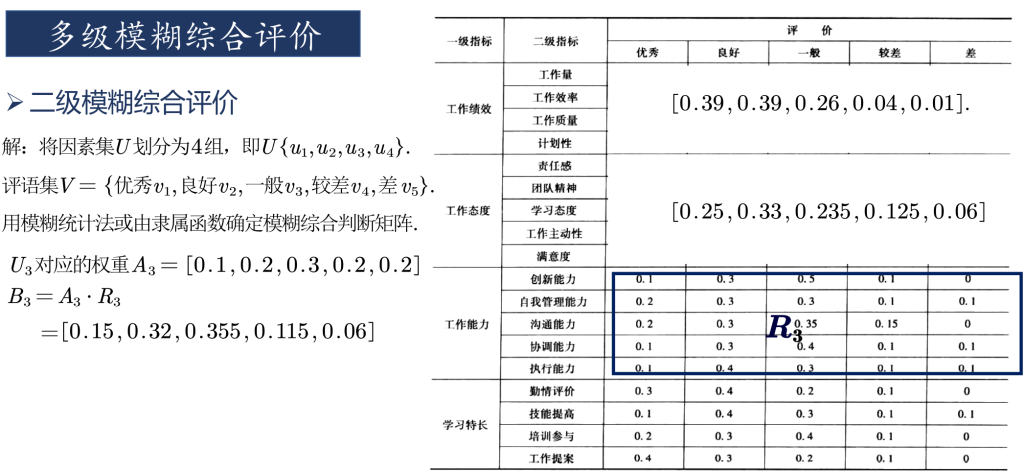
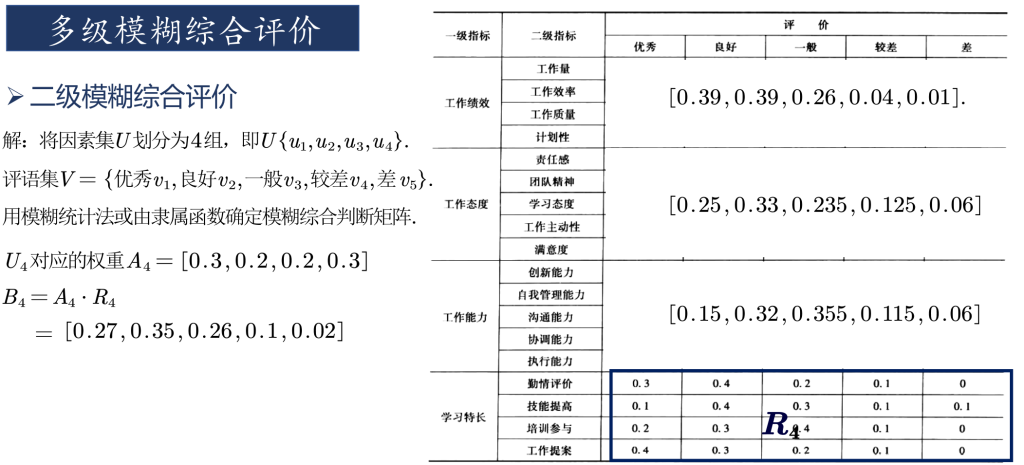
只有一级指标时,一级指标的评价分数由其他方法给出。划分出二级指标后,由其他方法给出二级指标的评价分数。下图即为某位员工的二级指标打分情况。将一级评判的结果作为一级指标的打分。具体步骤可见程序。
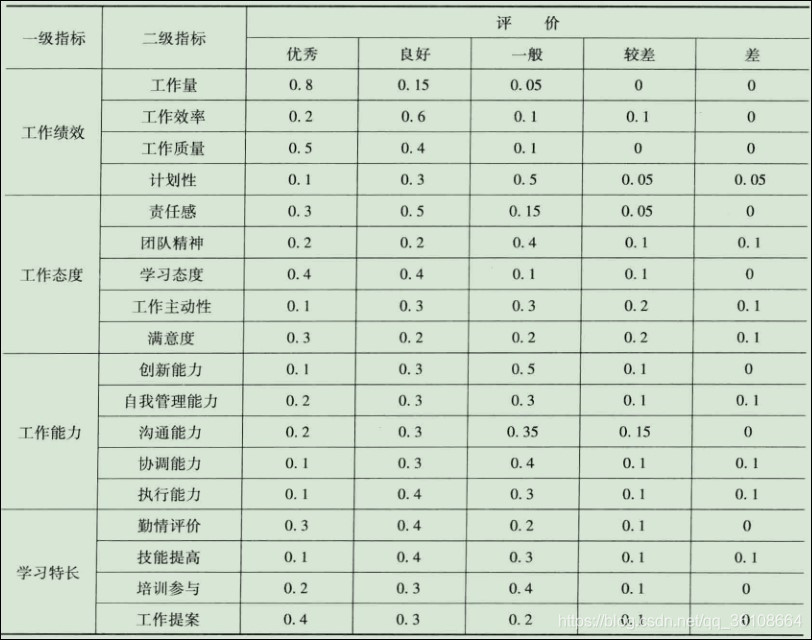
待处理数据
复制以下数据并保存在mhdata.txt文件中,即上图中的二级指标打分表。
0.8 0.15 0.05 0 0
0.2 0.6 0.1 0.1 0
0.5 0.4 0.1 0 0
0.1 0.3 0.5 0.05 0.05
0.3 0.5 0.15 0.05 0
0.2 0.2 0.4 0.1 0.1
0.4 0.4 0.1 0.1 0
0.1 0.3 0.3 0.2 0.1
0.3 0.2 0.2 0.2 0.1
0.1 0.3 0.5 0.1 0
0.2 0.3 0.3 0.1 0.1
0.2 0.3 0.35 0.15 0
0.1 0.3 0.4 0.1 0.1
0.1 0.4 0.3 0.1 0.1
0.3 0.4 0.2 0.1 0
0.1 0.4 0.3 0.1 0.1
0.2 0.3 0.4 0.1 0
0.4 0.3 0.2 0.1 0
原代码
书中实现代码如下
其运算的过程是简单的矩阵运算,在前面的步骤介绍中也是B = A·R,由矩阵的相乘得到评判结果。
clc, clear
a=load('mhdata.txt');
% 一级指标权重
w=[0.4 0.3 0.2 0.1];
% 二级指标权重
w1=[0.2 0.3 0.3 0.2];
w2=[0.3 0.2 0.1 0.2 0.2];
w3=[0.1 0.2 0.3 0.2 0.2];
w4=[0.3 0.2 0.2 0.3];
% 对子因素进行一级模糊综合评判
b(1,:)=w1a([1:4],:); b(2,:)=w2a([5:9],:);
b(3,:)=w3a([10:14],:); b(4,:)=w4a([15:end],:);
% 进行二级模糊综合评判,c即为评判结果
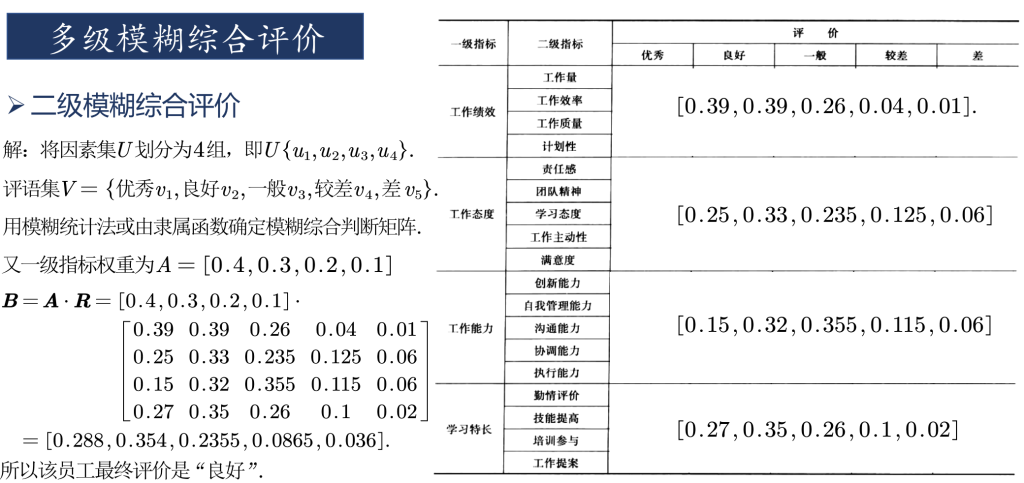
c=w*b运行结果为“优秀、良好、一般、较差、差”五个评价等级的打分
c =
0.2880 0.3540 0.2355 0.0865 0.0360
可以看到,综合评价结果在“良好”一项分数最高,根据最大隶属度原则,可以认为对该员工的评价良好。
改进代码
clc, clear
a=load('mhdata.txt');
% 一级指标权重
w=[0.4 0.3 0.2 0.1];
% 二级指标权重,对应4个一级指标
w1=[0.2 0.3 0.3 0.2];
w2=[0.3 0.2 0.1 0.2 0.2];
w3=[0.1 0.2 0.3 0.2 0.2];
w4=[0.3 0.2 0.2 0.3];
%% 一级模糊综合评判
b1 = []; %保存一级评判结果
w0 = w1'; %指标权重应为列向量m*1
b0 = a([1:4],:); %指标应与列向量对应m*n
% 以下为固定操作,进行模糊运算
c0 =[]; %临时结果
for i =1:max(size(b0))
for j= 1:max(size(w0))
c0(j,i)= min(w0(j,:),b0(j,i));
end
c0(j+1,i) = max(c0(:,i));
end
b1(1,:) = c0(j+1,:);
w0 = w2'; %指标权重应为列向量m*1
b0 = a([5:9],:); %指标应与列向量对应m*n
c0 =[];%临时结果
for i =1:max(size(b0))
for j= 1:max(size(w0))
c0(j,i)= min(w0(j,:),b0(j,i));
end
c0(j+1,i) = max(c0(:,i));
end
b1(2,:) = c0(j+1,:);
w0 = w3'; %指标权重应为列向量m*1
b0 = a([10:14],:); %指标应与列向量对应m*n
c0 =[];%临时结果
for i =1:max(size(b0))
for j= 1:max(size(w0))
c0(j,i)= min(w0(j,:),b0(j,i));
end
c0(j+1,i) = max(c0(:,i));
end
b1(3,:) = c0(j+1,:);
w0 = w4'; %指标权重应为列向量m*1
b0 = a([15:end],:); %指标应与列向量对应m*n
c0 =[];%临时结果
for i =1:max(size(b0))
for j= 1:max(size(w0))
c0(j,i)= min(w0(j,:),b0(j,i));
end
c0(j+1,i) = max(c0(:,i));
end
b1(4,:) = c0(j+1,:);
%% 二级模糊综合评判
w0 = w';
b0 = b1;
c0 =[];
for i =1:max(size(b0))
for j= 1:max(size(w0))
c0(j,i)= min(w0(j,:),b0(j,i));
end
c0(j+1,i) = max(c0(:,i));
end
c2 = c0(j+1,:)%二级评判结果
运行结果与原代码有区别,但是大体趋势相似。对此员工的综合评价在优秀和良好之间。
c2 =
0.3000 0.3000 0.2000 0.2000 0.1000
一些补充
模糊集合的概念
模糊集合用来描述形容高矮胖瘦这种没有明确指标的模糊性问题。不具有传统集合的互异性,
而是“亦此亦彼”的。

模糊集合的表示方法

模糊集合与特征函数的关系

模糊集合分类
- 极小型(小的概率大)
- 中间型(中间的概率大)
- 极大型(大的概率大)
F分布确定隶属函数


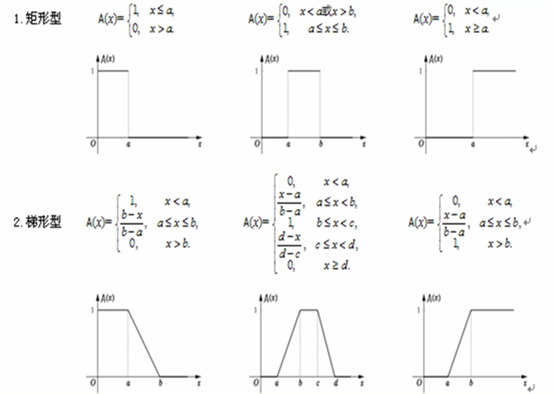
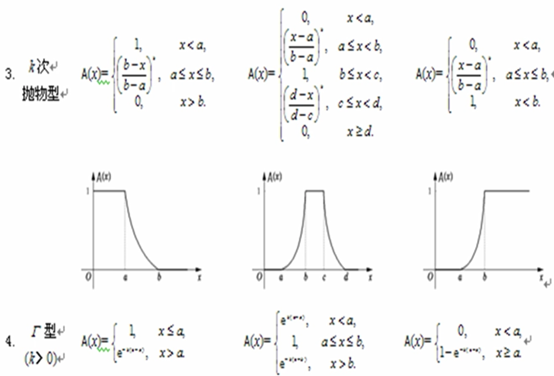
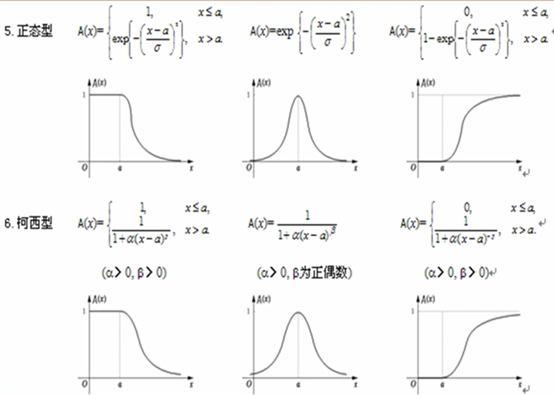
图像来源:(10条消息) 模糊数学 1、模糊集、隶属度函数、如何确定隶属度函数_中南自动化学院“智能控制与优化决策“至渝的博客-CSDN博客以及(10条消息) 模糊数学模型(一): 隶属函数、模糊集合的表示方法、模糊关系、模糊矩阵_wamg潇潇的博客-CSDN博客
三分法确定隶属函数


什么是模糊综合评价



行代表的是因素集中的元素(也就是需要判断的模糊概念),列表示评语集的元素,就是对因素的评价,r表示的就是描述改因素评语的隶属度
一级模糊评价


另外一个题目
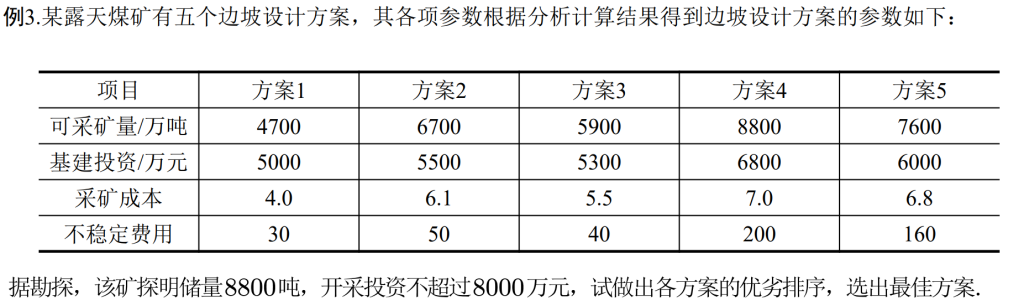


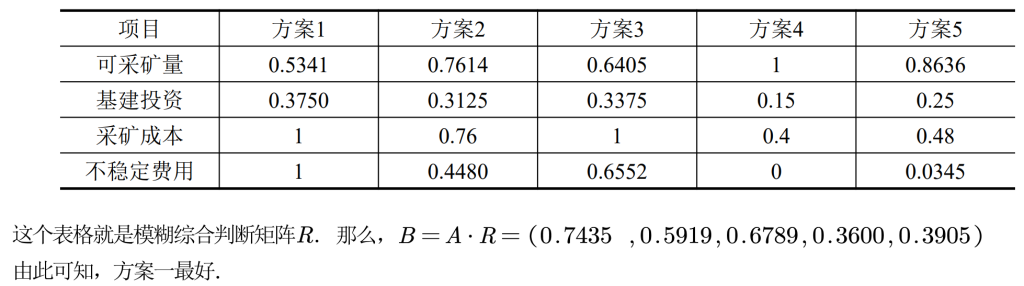
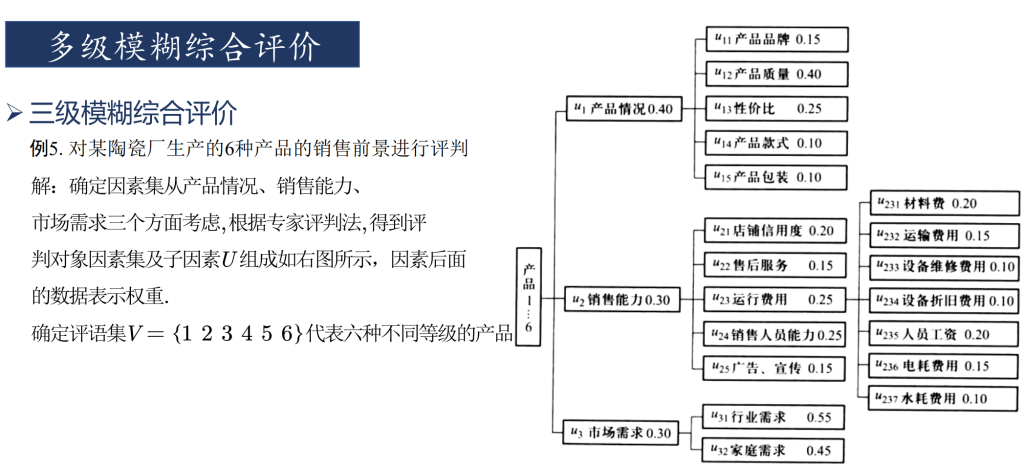
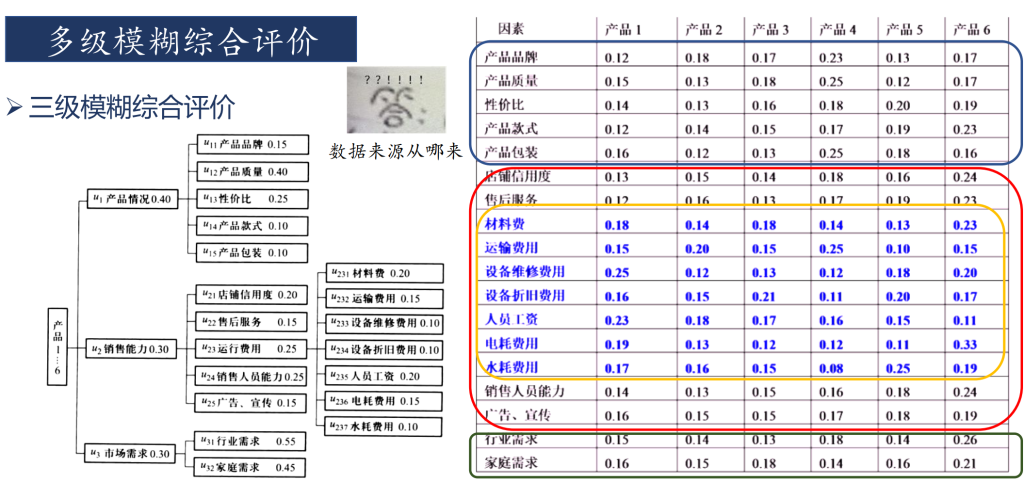
多级模糊评价

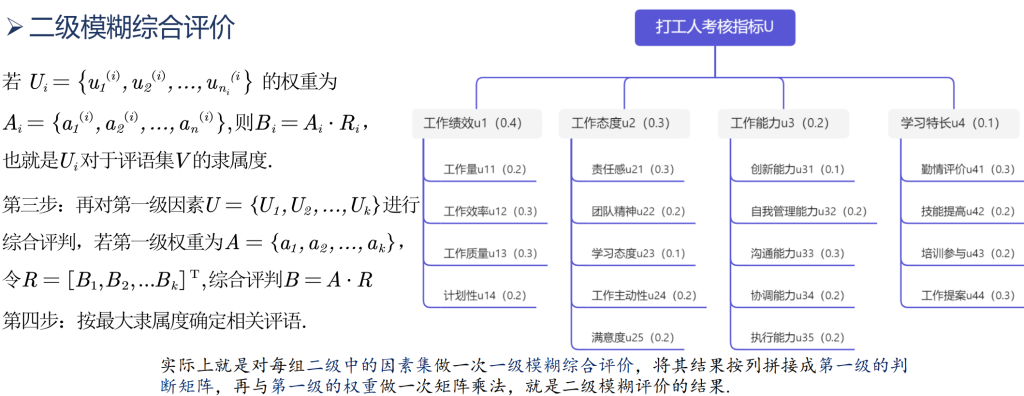
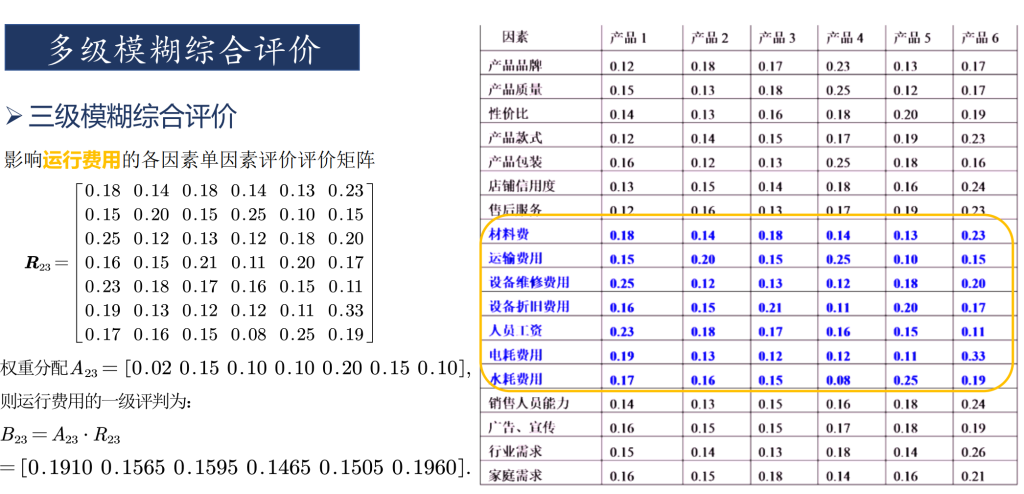
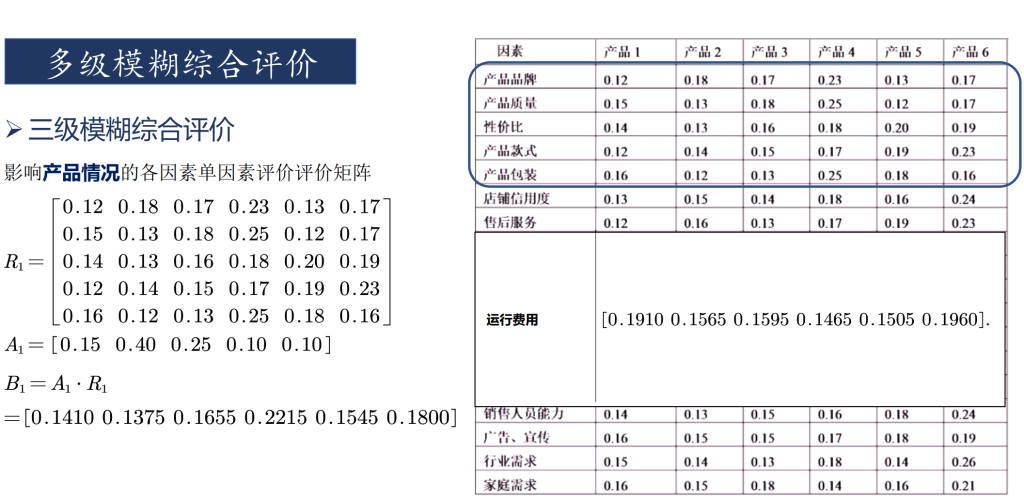
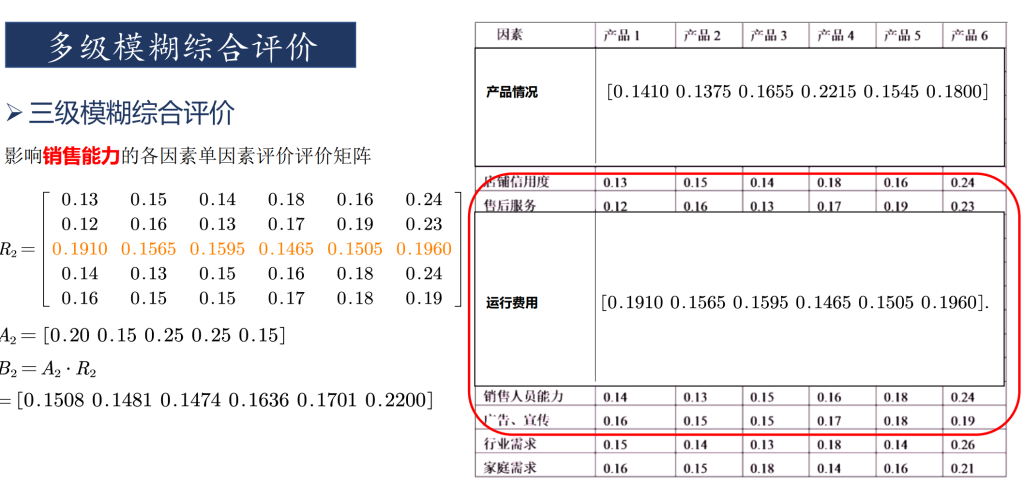
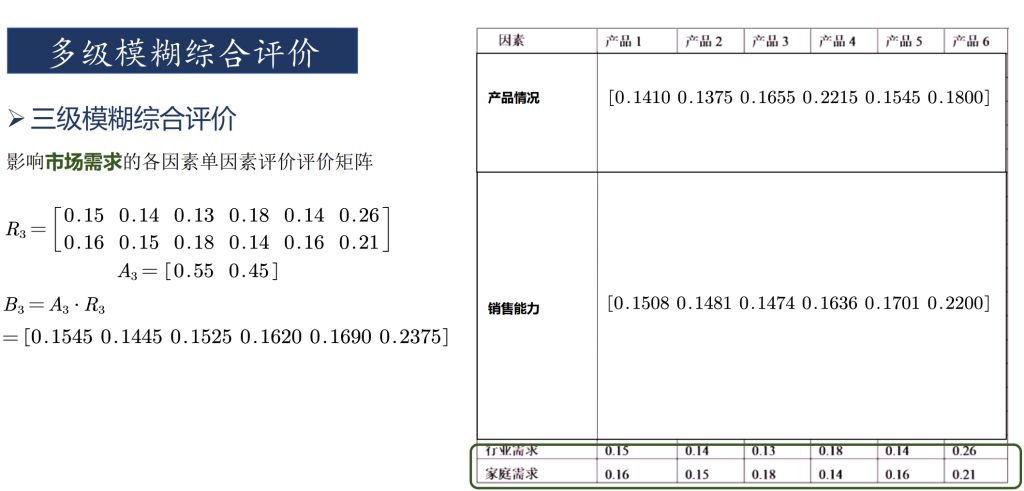
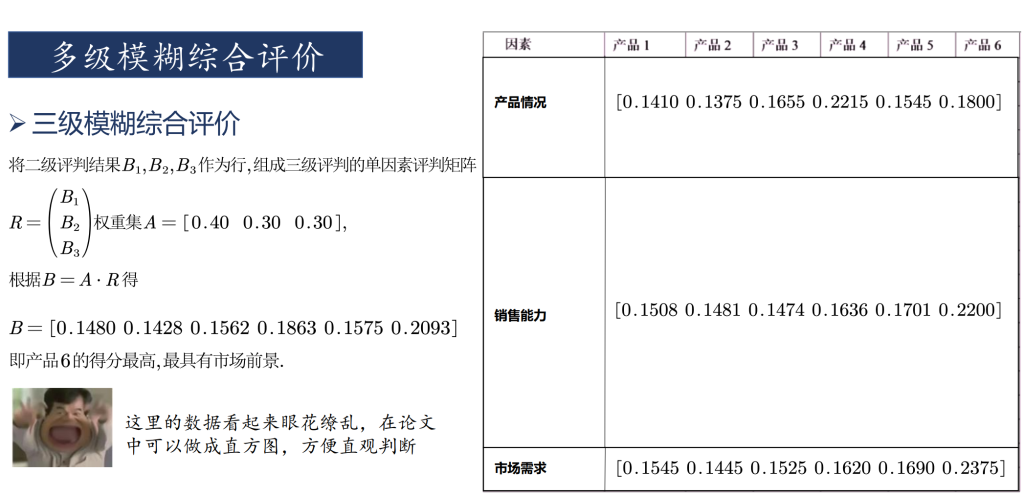
总结


熵权法
指标的变异程度越小,所反映的现有信息量也越少,其对应的权值也越低。也就是说,熵权法是使用指标内部所包含的信息量,来确定该指标在所有指标之中的地位。由于熵衡量着系统的混乱程度,也可以拿来衡量信息的多少,方法被命名为熵权法倒也可以理解。(不过都是我猜的……)
概率与信息量
如果小明同学的成绩一直是全校第一,小张同学的成绩一直是全校倒数第一,它们两个同时考取了清华大学。你觉得是“小明考上清华”这一事件的信息量比较大,还是“小张考上清华”这一事件的信息量比较大。很明显,“小张考上清华”这一事件中可能包含着更多的信息量。因为小明一直是全校第一,考上清华应该是一件自然而然的事情,大家都这么觉得。而小张一直是倒数第一,突然考上了清华,一件本来不可能发生的事情发生了,这里面就蕴含着许多的信息。
- 概率P(x)越小,信息量I(x)越大,原先掌握的信息越不靠谱
- 概率P(x)越大,信息量I(x)越小,原先掌握的信息很靠谱
所以我们定义I(x)=-ln(p(x))
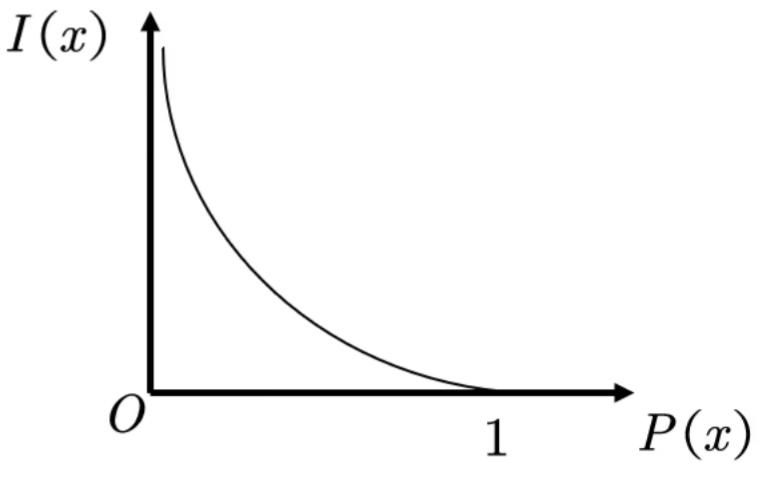
信息熵
熵:描述混乱程度的量钢
信息熵:平均而言发生一个事件我们得到的信息量大小(得到的信息越多,已掌握的信息越少)
熵权法:是一种可以对多对象,多指标进行综合评价的方法,其评价依据来源于数据本身,几乎不受主管因素的干扰
基本思想:信息熵小——得到的信息少,掌握的信息多——这组信息越靠谱——权重大
信息熵是对信息的期望值,那应该是信息熵越大,现有信息量越大吧。其实不然,因为这里的信息的期望值,应该是对未来潜在信息的一种期望。我们说小概率事件包含的信息量多,是因为一件几乎不可能发生的事件发生了,背后很大程度上有着许许多多未被挖掘的信息,最终导致了小概率事件的发生。我们说一件大概率事件包含的信息量少,其实也是指这件大概率事件发生后,能够被挖掘出的信息量比较少。
信息熵的定义


信息熵定性分析
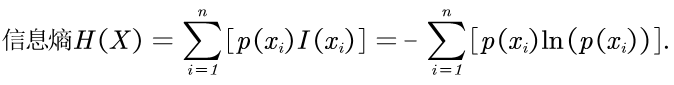

熵权法步骤
第一步:正向化处理
将区间型转化为极大型(就是数值越大越好的类型):数值不要太大也不要太小,落在某个区间最好,如人体的温度值落在36~37℃最好。设一组区间型指标{xi},其最佳区间为[a,b],那么可以这样正向化:
先算其最值到边界的最大举例M=max{a-min{xi},max{xi}-b}

| 体温 | 正向化后的体温 |
| 35.2 | 0.2 |
| 35.8 | 0.8 |
| 36.5 | 1 |
| 37.2 | 0.8 |
| 38.0 | 0 |
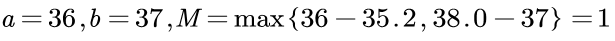
第二步:标准化处理
为了可以一起计算,要消除单位的影响,也就是消除量纲


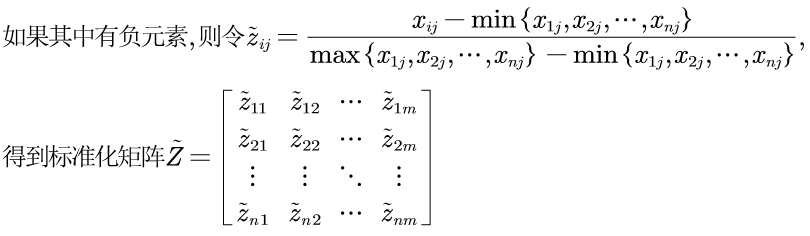

第三步:计算信息熵和熵权
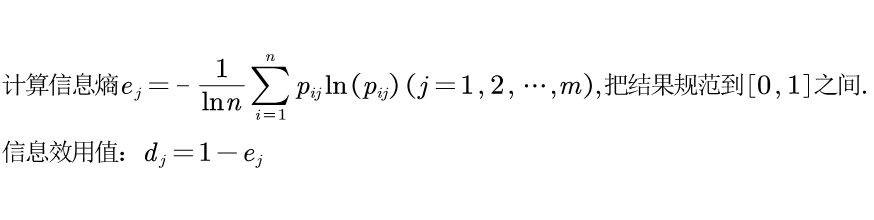
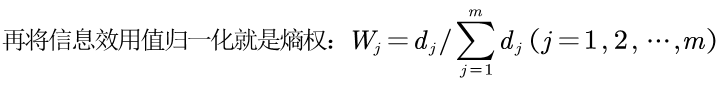
TOPSIS优劣解距离法
距离法,就是将整个过程中某一个位置与起点的距离比上整个过程的距离得到的比值就是距离法得到的数值
模型适用条件
- 选择最优策略,最佳人选问题
- 评价的决策层很多,即n很大
- 决策层中指标的数据是已知的
TOPSIS步骤
将原始矩阵正向化
将所有指标类型统一转为极大型指标
常见指标类型:
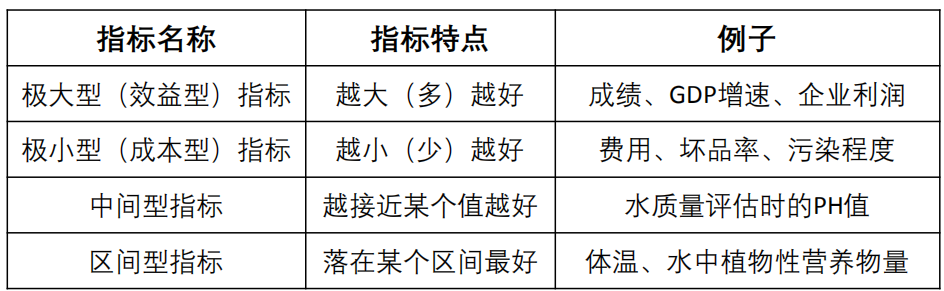
极小型指标正向化
- 公式:max-x
- 如果所有元素均为正数,也可使用1/x
中间型指标正向化
- 公式:

区间型指标正向化

正向化矩阵标准化
目的:消除不同量纲的影响

计算得分并归一化

注:用层次分析法来确定权重(熵权法也可以)
灰色关联分析法
定义
灰色关联分析是根据因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法【若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低】
当样本个数 n 较大时,用标准化回归(第7讲学),当样本个数 n 较少时,用灰色关联分析
灰色关联分析用来确定一个系统中,哪些因素是主要因素,哪些因素是次要因素,哪些对系统发展影响大,哪些因素对系统发展影响小,从而进行系统分析,强化推动因素,抑制阻碍因素。
原理
根据序列曲线几何形状的相似度来判断联系是否紧密。曲线越接近,相应序列之间的关联度就越大,反而就越小。
前要
数据预处理
此处的数据预处理可以用之前的标准化,也可以用指标内每一个数除以指标所有数的平均值
目的都是消除量纲的影响
| 年份 | 结婚对数 | 房价 | 人均收入 | 女性失业数 |
| 2017 | 3806 | 398 | 850 | 1352 |
| 2018 | 3356 | 455 | 846 | 1268 |
| 2019 | 2750 | 482 | 960 | 1010 |
| 2020 | 2335 | 422 | 900 | 953 |
| 2021 | 2061 | 561 | 1024 | 808 |
| 2022 | 1988 | 511 | 1100 | 763 |
| 结婚对数 | 房价 | 人均收入 | 女性失业数 | |
| 2017 | 1.4013 | 0.8441 | 0.8979 | 1.3182 |
| 2018 | 1.2356 | 0.9650 | 0.8937 | 1.2363 |
| 2019 | 1.0125 | 1.0223 | 1.0141 | 0.9847 |
| 2020 | 0.8597 | 0.8950 | 0.9507 | 0.9292 |
| 2021 | 0.7588 | 1.1898 | 1.0817 | 0.7878 |
| 2022 | 0.7320 | 1.0838 | 1.1620 | 0.7439 |
确定分析序列
参考数列(母序列):能够反映系统行为特征的数据序列,记作x0
比较序列(子序列):影响系统行为的因素组成的数据序列,记作xi(i = 1,2,...,n)
例如结婚率就是参考数列,放假,人均收入,女性失业率就是比较数列
可以理解为参考数列类似因变量y,比较数列是对应的自变量x
确定灰色关联系数
定义两级最小差a = mins mint |x0(t)-xs(t)|,以及两级最大差b = maxs maxt|x0(t)-xs(t)|
| 结婚对数(x0) | 房价(x1) | 人均收入(x2) | 女性失业数(x3) | |
| 2017 | 1.4013 | 0.8441 | 0.8979 | 1.3182 |
| 2018 | 1.2356 | 0.9650 | 0.8937 | 1.2363 |
| 2019 | 1.0125 | 1.0223 | 1.0141 | 0.9847 |
| 2020 | 0.8597 | 0.8950 | 0.9507 | 0.9292 |
| 2021 | 0.7588 | 1.1898 | 1.0817 | 0.7878 |
| 2022 | 0.7320 | 1.0838 | 1.1620 | 0.7439 |
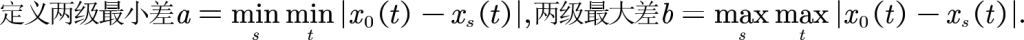
| |X0-x1| | |X0-x2| | |X0-x3| | |
| 2017 | 0.5572 | 0.5034 | 0.0832 |
| 2018 | 0.2706 | 0.3420 | 0.0006 |
| 2019 | 0.0098 | 0.0016 | 0.0278 |
| 2020 | 0.0353 | 0.0910 | 0.0694 |
| 2021 | 0.4310 | 0.3229 | 0.0289 |
| 2022 | 0.3518 | 0.4300 | 0.0119 |
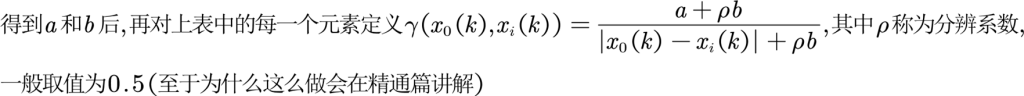
| Gamma(X0,x1) | Gamma(X0,x2) | Gamma(X0,x3) | |
| 2017 | 0.3341 | 0.3571 | 0.7719 |
| 2018 | 0.5084 | 0.4500 | 1.0000 |
| 2019 | 0.9684 | 0.9967 | 0.9113 |
| 2020 | 0.8896 | 0.7555 | 0.8023 |
| 2021 | 0.3935 | 0.4643 | 0.9079 |
| 2022 | 0.4429 | 0.3941 | 0.9610 |

| Gamma(X0,x1) | Gamma(X0,x2) | Gamma(X0,x3) | |
| 2017 | 0.3341 | 0.3571 | 0.7719 |
| 2018 | 0.5084 | 0.4500 | 1.0000 |
| 2019 | 0.9684 | 0.9967 | 0.9113 |
| 2020 | 0.8896 | 0.7555 | 0.8023 |
| 2021 | 0.3935 | 0.4643 | 0.9079 |
| 2022 | 0.4429 | 0.3941 | 0.9610 |
| 灰色关联度 | 0.5895 | 0.5696 | 0.8924 |

定义
步骤
- 正向化(若已经全是极大型 则不需要)
- 预处理(每一个元素都被预处理)
- 构造母序列和子序列(若题目本身已给出 则不需要)
- 计算各个指标与母序列的灰色关联度(每一列 都可以求出一个灰色关联度)
- 针对各个指标的权重 计算每一个元素的得分(若每一列的灰色关联度都一样 则不需要)
- 对得分进行归一化 并排序
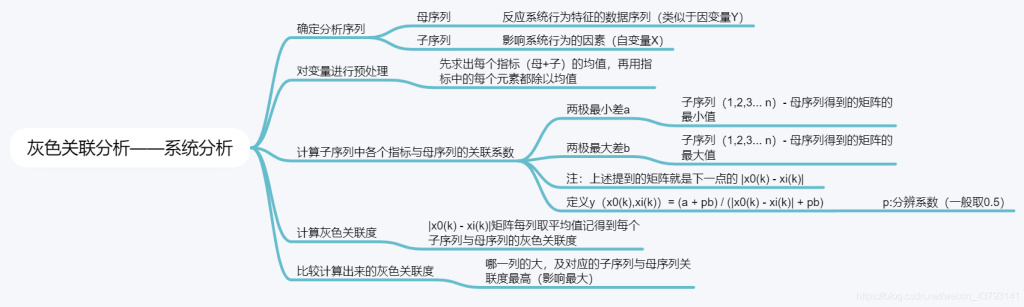
使用灰色关联分析的两种套路
① 用于系统分析(比较母序列与哪个子序列最接近)
我们以下图举例,分析国内生产总值与哪一个产业的影响最大?
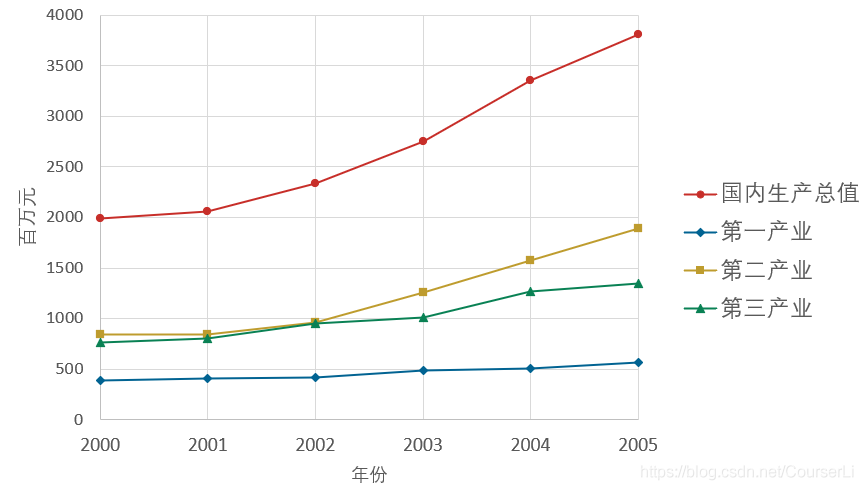
load gdp.mat
% 导入数据
Mean = mean(gdp);
% 求出每一列的均值以供后续的数据预处理
gdp = gdp ./ repmat(Mean,size(gdp,1),1);
% 将矩阵进行复制为和gdp同等大小,然后使用点除(对应元素相除)
disp('预处理后的矩阵为:'); disp(gdp)
Y = gdp(:,1);
% 母序列
X = gdp(:,2:end);
% 子序列
absX0_Xi = abs(X - repmat(Y,1,size(X,2))) % 计算|Y-Xi|矩阵
a = min(min(absX0_Xi))
% 计算两级最小差a
b = max(max(absX0_Xi))
% 计算两级最大差b
rho = 0.5;
% 分辨系数取 0.5
gamma = (a+rho*b) ./ (absX0_Xi + rho*b)
% 计算子序列中各个指标与母序列的关联系数
disp('子序列中各个指标的灰色关联度分别为:')
disp(mean(gamma))
② 用于综合评价模型(评价哪个子序列是最优解)

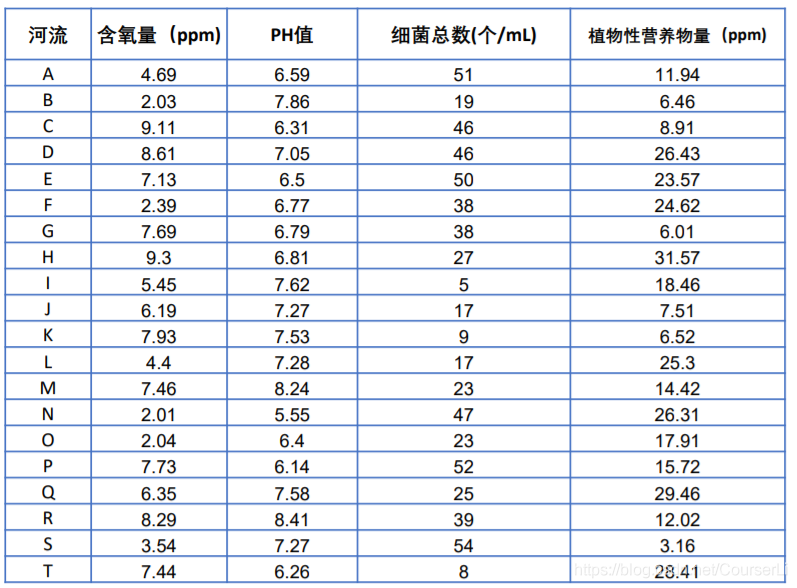
load data_water_quality.mat
% 导入数据
...
% 进行正向化(操作就省略了)
%% 对正向化后的矩阵进行预处理
Mean = mean(X);
% 求出每一列的均值以供后续的数据预处理
Z = X ./ repmat(Mean,size(X,1),1);
disp('预处理后的矩阵为:'); disp(Z)
%% 构造母序列和子序列
Y = max(Z,[],2);
% 母序列为虚拟的,用每一行的最大值构成的列向量表示母序列
X = Z;
% 子序列就是预处理后的数据矩阵
%% 计算得分
absX0_Xi = abs(X - repmat(Y,1,size(X,2)))
% 计算|X0-Xi|矩阵
a = min(min(absX0_Xi))
% 计算两级最小差a
b = max(max(absX0_Xi))
% 计算两级最大差b
rho = 0.5; % 分辨系数取0.5
gamma = (a+rho*b) ./ (absX0_Xi + rho*b)
% 计算子序列中各个指标与母序列的关联系数
weight = mean(gamma) / sum(mean(gamma));
% 利用子序列中各个指标的灰色关联度计算权重
score = sum(X .* repmat(weight,size(X,1),1),2);
% 未归一化的得分
stand_S = score / sum(score);
% 归一化后的得分
[sorted_S,index] = sort(stand_S ,'descend')
% 进行排序
对于这题,我们需要自己构造母序列和子序列,每一行的最大值构成的列向量表示母序列,而预处理后的矩阵表示子序列,接下来,就可以比较母序列与哪个子序列最接近了
补充
一般情况下母序列只有一个,但若母序列含有多个,则每个母序列都要与子序列算一遍,算出的灰色关联度,再来求平均值
灰色关联分析的评估
- 灰色关联分析的优势:
- (1)因此对样本量的多少没有过多的要求,也不需要典型的分布规律,而且计算量比较小,其结果与定性分析结果会比较吻合。
- (2)是系统分析中比较简单、可靠的一种分析方法
- 灰色关联分析的缺点:
- (1)随着灰色关联分析理论应用领域的不断扩大,现有的一些模型存在的不足之处使得其不能很好地解决某些方面的实际问题
- (2)整个理论体系目前还不是很完善,其应用受到了某些限制
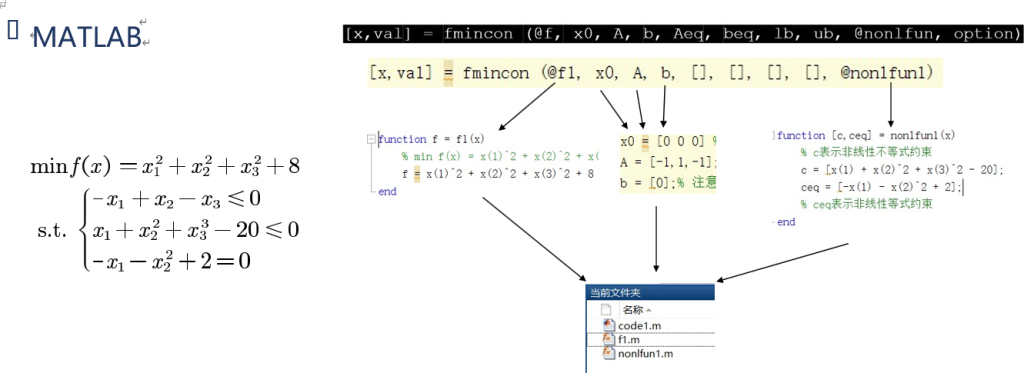
非线性规划
定义
其实就是不是线性函数的求解... ...比如未知数带二次方或者三次方之类的

matlab求解函数

[x,val] = fmincon (@f, x0, A, b, Aeq, beq, lb, ub, @nonlfun, option)| @f | 表示引用定义在外部的目标函数 |
| x0 | 初始值x0必须有,因为求出来的是局部最优解 |
| option | 表示所用的求解方法,有interior-point(内点法)、 sqp(序列二次规范法)、active-set(有效集法)、 trust-region-reflective(信赖域反射算法) |
| @nonlcun | 调用一个定义在外部的非线性部分的约束 (只是为了教学,当然也可以定义在脚本内部) |
@f为定义的需要求的目标函数捏
| A,b | 线性不等式系数矩阵和常数向量 |
| Aeq,beq | 线性等式的系数矩阵和常数向量 |
| lb,ub | 决策变量的最小值和最大值 |
| x | 取得目标函数最小值时x的取值 |
| val | 目标函数的最小值 |
| [] | 如果不存在某项约束则在对应位置填‘[]’ |
| +inf,-inf | 若某个x无上下界则在对应矩阵上填此项 |
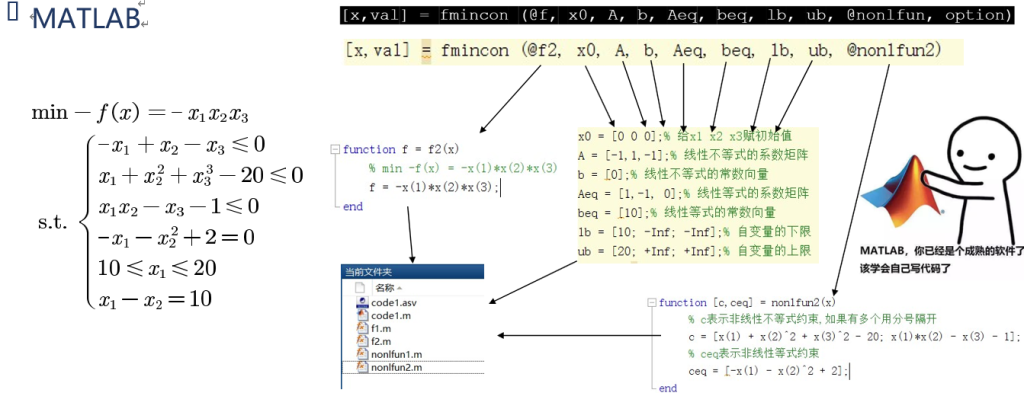
图论
图的定义
将平面上若干点用曲线或直线连接起来不考虑点的位置与连线曲直长短,这样形成的关系结构就是图,例如:
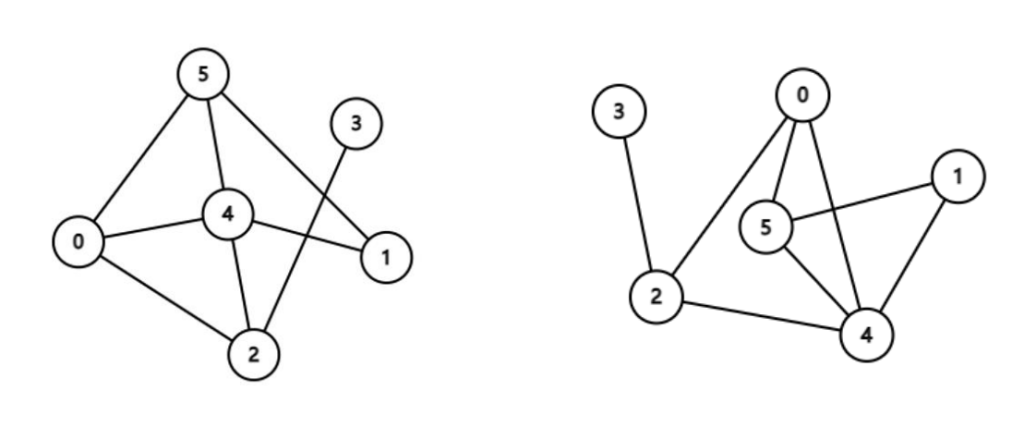
类型
有向图和无向图,例如、
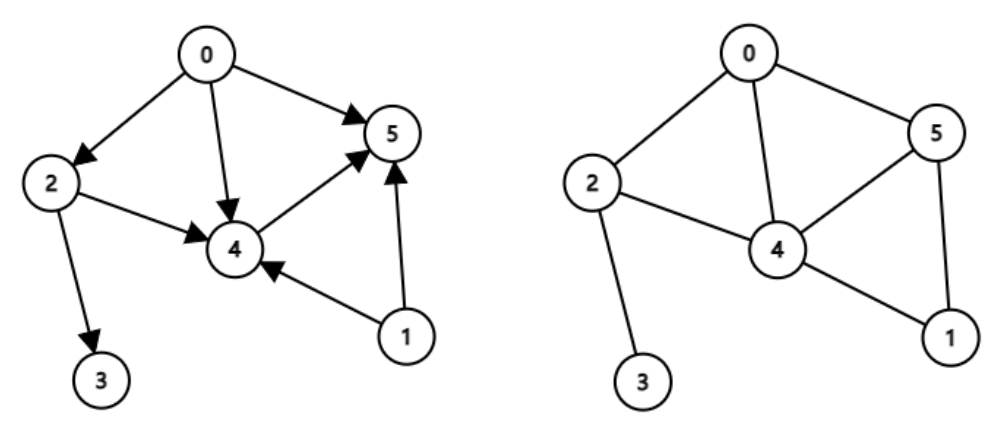
表示方法
图可以被表示为 G={V, E},其中 V={v1, ... , vN},E= {e1, ... , eM}。
其中V(vertex)表示顶点集,E(edge)表示边集
图的数据结构
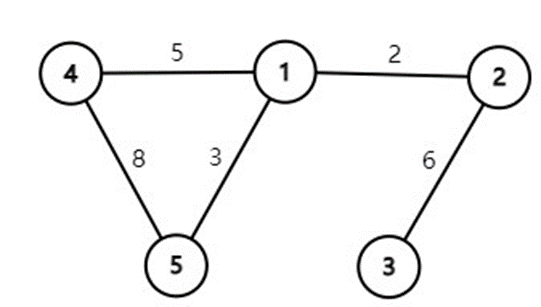
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 2 | Inf | 5 | 3 |
| 2 | 0 | ||||
| 3 | 0 | ||||
| 4 | 0 | ||||
| 5 | 0 |
没有距离数据以Inf填写
反思
迪杰斯特拉算法采用贪心策略,只顾眼前最优解而不顾未来,所以我们可以采用先抛弃distance直接对所有边进行更新最短路径和前驱节点的操作(有n个顶点,每一次循环都要做n-1次更新操作),这就是贝尔曼福特算法的思想,当然复杂度会提高
还有一种算法是动态规划的思想,弗洛伊德算法就是基于“跳板城市”的技巧,加入其他的节点作为中间跳板然后选择最短的一条~~~
迪杰斯特拉算法matlab实现
[P,d] = shortestpath (G, start, end, [’method’, algorithm])| G | 要求解的图 |
| start | 起始节点 |
| end | 目标节点 |
| [’method’, algorithm] | 求解方法 |
| P | 最短路径经过的节点序列 |
| d | 最短距离 |
| ‘auto’ | 默认值,使用该项会自动选择算法,其中有 1.‘unweighted‘ 用于无权重图的求解 2.‘positive‘ 用于有权重的图的求解,但要求其边权重为非负数 |
| ‘unweighted’ | 用宽搜(广度优先)求解(仅适用于无权图) |
| ‘postive’ | 用Dijkstra算法求解 |
| ‘mixed’ | 用贝尔曼-福特算法求解 |
持续学习中...持续更新中...






Comments NOTHING